
分析 先根据分式的加减法则计算出等式右边的值,两边相比较即可得出结论.
解答 解:∵右边=$\frac{Ax(x-2)+B(x-2)+{cx}^{2}}{{x}^{2}(x-2)}$=$\frac{{Ax}^{2}-2Ax+Bx-2B+{cx}^{2}}{{x}^{2}(x-2)}$=$\frac{{(A+C)x}^{2}-(2A-B)x-2B}{{x}^{2}(x-2)}$,
∴$\left\{\begin{array}{l}A+C=2\\-2A+B=4\\ 2B=5\end{array}\right.$,解得$\left\{\begin{array}{l}A=\frac{11}{4}\\ B=\frac{5}{2}\\ C=-\frac{3}{4}\end{array}\right.$,
∴A+B+C=$\frac{11}{4}$+$\frac{5}{2}$-$\frac{3}{4}$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查的是分式的加减法,熟知异分母的分式相加减的法则是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
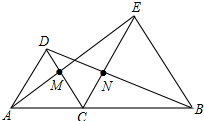 如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:
如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
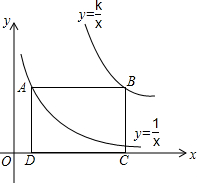 如图,点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,C,D两点在x轴上.若矩形ABCD的面积为6,求B点所在双曲线的函数表达式.
如图,点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,C,D两点在x轴上.若矩形ABCD的面积为6,求B点所在双曲线的函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
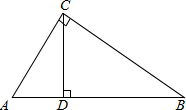 如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com