
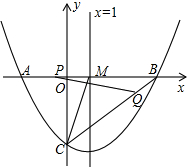
 如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.分析 (1)利用待定系数法求得即可;
(2)根据解析式求得B、C的坐标,求得OB=4,OC=3,进而求得BM=3,BC=5,得出BP=6-3t,BQ=2t,若△BPQ∽△BCM,则$\frac{6-3t}{5}$=$\frac{2t}{3}$,解得t=$\frac{18}{19}$;若△BQP∽△BCM,则$\frac{2t}{5}$=$\frac{6-3t}{3}$,解得t=$\frac{10}{7}$;
(3)利用待定系数法求得直线BC的解析式,根据题意求得BQ=4,根据三角形相似求得Q($\frac{4}{5}$,-$\frac{12}{5}$),当BQ是平行四边形的边时,E的横坐标为$\frac{21}{5}$或-$\frac{11}{5}$,代入抛物线的解析式为y=$\frac{93}{200}$,当BQ是平行四边形的对角线时,E的横坐标为$\frac{19}{5}$,代入抛物线的解析式为y=-$\frac{87}{200}$;所以E的坐标为($\frac{21}{5}$,$\frac{93}{200}$)或(-$\frac{11}{5}$,$\frac{93}{200}$)或($\frac{19}{5}$,-$\frac{87}{200}$).
解答 解:(1)根据题意得$\left\{\begin{array}{l}{4a-2b-3=0}\\{-\frac{b}{2a}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{8}}\\{b=-\frac{3}{4}}\end{array}\right.$
∴抛物线的解析式为y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3;
(2)由y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3可知B(4,0),C(0-3),
∴OB=4,OC=3,
∴BM=3,BC=5,
∴BP=6-3t,BQ=2t
若△BPQ∽△BCM,则$\frac{BP}{BC}$=$\frac{BQ}{BM}$,得$\frac{6-3t}{5}$=$\frac{2t}{3}$,解得t=$\frac{18}{19}$;
若△BQP∽△BCM,则$\frac{BQ}{BC}$=$\frac{BP}{BM}$,得$\frac{2t}{5}$=$\frac{6-3t}{3}$,解得t=$\frac{10}{7}$;
(3)∵B(4,0),C(0-3),
∴直线BC解析式:y=$\frac{3}{4}$x-3,
当t=2时,P到达终点B,BQ=4,
作QN⊥AB于N,
∴△BQN∽△BCO,
∴$\frac{QN}{OC}$=$\frac{BQ}{BC}$,即$\frac{QN}{3}$=$\frac{4}{5}$,
∴QN=$\frac{12}{5}$,
∴Q的纵坐标为-$\frac{12}{5}$,
代入y=$\frac{3}{4}$x-3,得x=$\frac{4}{5}$,
∴Q($\frac{4}{5}$,-$\frac{12}{5}$),
当BQ是平行四边形的边时,
∵对称轴直线x=1,
∵Q的对称轴的距离为$\frac{1}{5}$,
∴E的横坐标为$\frac{16}{5}$+1=$\frac{21}{5}$或-$\frac{16}{5}$+1=-$\frac{11}{5}$,
代入抛物线的解析式为y=$\frac{93}{200}$,
∴E1($\frac{21}{5}$,$\frac{93}{200}$),E2(-$\frac{11}{5}$,$\frac{93}{200}$),
当BQ是平行四边形的对角线时,
∵B点到对称轴的距离为3,
∴E的横坐标为3+$\frac{4}{5}$=$\frac{19}{5}$,
代入抛物线的解析式为y=-$\frac{87}{200}$;
∴${E_3}(\frac{19}{5},-\frac{87}{200})$,
综上,在(2)的条件下,当点运动停止时,存在点E、F,使得以B、Q、E、F为顶点的四边形是平行四边形,此时E的坐标为($\frac{21}{5}$,$\frac{93}{200}$)或(-$\frac{11}{5}$,$\frac{93}{200}$)或($\frac{19}{5}$,-$\frac{87}{200}$).
点评 本题是二次函数的综合题,考查了待定系数法求解析式,三角形相似的判定和性质,平行四边形的性质等,根据题意画出图形是解题的关键.


科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
计算(-a)3·(a2)3·(-a)2的结果正确的是( )
A. -a11 B. a11 C. -a10 D. a13
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 荷花小区要在一块一边靠墙(墙长是15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,如图所示.若设花园BC的边长为xm,花园的面积为y m2.
荷花小区要在一块一边靠墙(墙长是15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,如图所示.若设花园BC的边长为xm,花园的面积为y m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 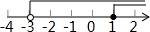 | C. |  | D. | 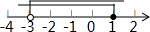 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
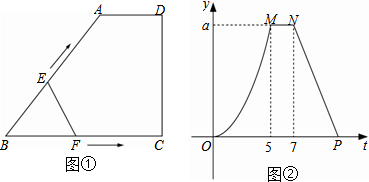
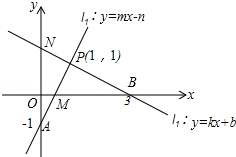 如图,请根据图象所提供的信息解答下列问题:
如图,请根据图象所提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com