
 如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.分析 (1)根据折叠的性质和矩形性质以得PD=PH=3,CD=MH=4,∠H=∠D=90°,然后利用勾股定理可计算出MP=5;
(2)如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,利用两点之间线段最短可得点F即为所求,过点E作EN⊥AD,垂足为N,则AM=AD-MP-PD=4,所以AM=AM′=4,再证明ME=MP=5,接着利用勾股定理计算出MN=3,所以NM′=11,然后证明△AFM′∽△NEM′,则可利用相似比计算出AF;
(3)如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,易得QE=GR,而GM=GM′,于是MG+QE=M′R,利用两点之间线段最短可得此时MG+EQ最小,于是四边形MEQG的周长最小,在Rt△M′RN中,利用勾股定理计算出M′R=5$\sqrt{5}$,易得四边形MEQG的最小周长值是7+5$\sqrt{5}$.
解答  解:(1)∵四边形ABCD为矩形,
解:(1)∵四边形ABCD为矩形,
∴CD=AB=4,∠D=90°,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴PD=PH=3,CD=MH=4,∠H=∠D=90°,
∴MP=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(2)如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,
∵AM=AD-MP-PD=12-5-3=4,
∴AM=AM′=4,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴∠CEP=∠MEP,
而∠CEP=∠MPE,
∴∠MEP=∠MPE,
∴ME=MP=5,
在Rt△ENM中,MN=$\sqrt{M{E}^{2}-N{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴NM′=11,
∵AF∥NE,
∴△AFM′∽△NEM′,
∴$\frac{M′A}{M′N}$=$\frac{AF}{EN}$,即$\frac{4}{11}$=$\frac{AF}{4}$,解得AF=$\frac{16}{11}$,
即AF=$\frac{16}{11}$时,△MEF的周长最小;
(3)如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,
∵ER=GQ,ER∥GQ,
∴四边形ERGQ是平行四边形,
∴QE=GR,
∵GM=GM′,
∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,
在Rt△M′RN中,NR=4-2=2,
M′R=$\sqrt{1{1}^{2}+{2}^{2}}$=5$\sqrt{5}$,
∵ME=5,GQ=2,
∴四边形MEQG的最小周长值是7+5$\sqrt{5}$.
点评 本题考查了几何变换综合题:熟练掌握折叠的性质和矩形的性质;会利用轴对称解决最短路径问题;会运用相似比和勾股定理计算线段的长.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
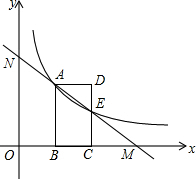 如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴上,A,D在第一象限,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,交CD于点E,OB=2,AB=3.
如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴上,A,D在第一象限,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,交CD于点E,OB=2,AB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
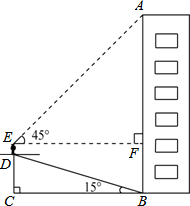 小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).
如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com