
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży£½ax2+bx+c£Øa£¾0£©µÄĶ¼Ļó¾¹żµćA£Ø1£¬2£©£®
£Ø1£©µ±b£½1£¬c£½©4Ź±£¬Ēóøƶž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©ŅŃÖŖµćM£Øt©1£¬5£©£¬N£Øt+1£¬5£©ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬ĒėÖ±½ÓŠ“³ötµÄȔֵ·¶Ī§£»
£Ø3£©µ±a£½1Ź±£¬Čōøƶž“ĪŗÆŹżµÄĶ¼ĻóÓėÖ±Ļßy£½3x©1½»ÓŚµćP£¬Q£¬½«“ĖÅ×ĪļĻßŌŚÖ±ĻßPQĻĀ·½µÄ²æ·ÖĶ¼Ļó¼ĒĪŖC£¬
¢ŁŹŌÅŠ¶Ļ“ĖÅ×ĪļĻߵĶ„µćŹĒ·ńŅ»¶ØŌŚĶ¼ĻóCÉĻ£æČōŹĒ£¬ĒėÖ¤Ć÷£»Čō²»ŹĒ£¬Ēė¾Ł·“Ąż£»
¢ŚŅŃÖŖµćP¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖįµÄ¶Ō³ĘµćĪŖP”䣬ČōP”äŌŚĶ¼ĻóCÉĻ£¬ĒóbµÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©y£½5x2+x©4£»£Ø2£©0£¼t£¼2£»£Ø3£©¢Ł²»ŹĒ£¬·“Ąż¼ū½āĪö£»¢Śb£¾4»ņb£¼©2£®
”¾½āĪö”æ
£Ø1£©½«µćAµÄ×ų±źŗĶb”¢cµÄÖµ“śČėy£½ax2+bx+cÖŠ±ćæÉĒóµĆaµÄÖµ£¬ĪŹĢā±ćæɽā¾ö£»
£Ø2£©ÓɵćM£¬NµÄ×ų±źĶĘ³öøƶž“ĪŗÆŹżµÄ¶Ō³ĘÖįŹĒÖ±Ļßx£½t£¬½įŗĻÅ×ĪļĻß £Øa£¾0£©æŖæŚĻņÉĻĶĘ³öµćM£¬N·Ö±šĀäŌŚµćA£Ø1£¬2£©µÄ×ó²ąŗĶÓŅ²ą£¬ÓÉ“ĖæÉĮŠ³ö¹ŲÓŚtµÄ²»µČŹ½×飬½ā“Ė²»µČŹ½×鼓æÉ£»
£Ø3£©¢ŁČē¾Ł·“ĄżÅ×ĪļĻßy£½x2+1ÓėÖ±Ļßy£½3x©1£¬ÅŠ¶ĻĖüĆĒÓŠĮ½øö½»µć£Ø¼“ĮŖĮ¢·½³Ģ×éÓŠĮ½×é²»Ķ¬µÄ½ā£©£¬²¢Ēó³öÅ×ĪļĻ߶„µć×ų±ź²»ŌŚÖ±Ļßy£½3x©1Ö®ĻĀ±ćæÉ£»
¢ŚŅŖŹ¹µćP¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖįµÄ¶Ō³ĘµćĪŖP”äŌŚĶ¼ĻóCÉĻ£¬Ōņ¶ž“ĪŗÆŹży£½ax2+bx+c£Øa£¾0£©Ķ¼ĻóµÄ¶„µć±ŲŌŚCÉĻ£¬Ōņµ±x£½©![]() Ź±£¬ax2+bx+c£¼3x©1£¬µĆµ½Ņ»øö¹ŲÓŚa”¢b”¢cµÄ²»µČŹ½£¬°Ńa£½1£¬A£Ø1£¬2£©“śČėy£½ax2+bx+c£Øa£¾0£©ÖŠ£¬ÓĆb±ķŹ¾c£¬ŌŁ°Ńa£½1Óėc“śČėĒ°ĆęµĆµ½µÄ¹ŲÓŚa”¢b”¢cµÄ²»µČŹ½ÖŠ£¬±ćæÉĒóµĆbµÄȔֵ·¶Ī§£®
Ź±£¬ax2+bx+c£¼3x©1£¬µĆµ½Ņ»øö¹ŲÓŚa”¢b”¢cµÄ²»µČŹ½£¬°Ńa£½1£¬A£Ø1£¬2£©“śČėy£½ax2+bx+c£Øa£¾0£©ÖŠ£¬ÓĆb±ķŹ¾c£¬ŌŁ°Ńa£½1Óėc“śČėĒ°ĆęµĆµ½µÄ¹ŲÓŚa”¢b”¢cµÄ²»µČŹ½ÖŠ£¬±ćæÉĒóµĆbµÄȔֵ·¶Ī§£®
½ā£ŗ£Ø1£©°ŃµćA£Ø1£¬2£©£®b£½1£¬c£½©4“śČė¶ž“ĪŗÆŹży£½ax2+bx+c£Øa£¾0£©£¬
µĆ£ŗ2£½a+1©4
”ąa£½5£¬b£½1£¬c£½©4£¬
”ą¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½ĪŖy£½5x2+x©4£»
£Ø2£©”ßµćM£Øt©1£¬5£©£¬N£Øt+1£¬5£©ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬
”ąøƶž“ĪŗÆŹżµÄ¶Ō³ĘÖįŹĒÖ±Ļßx£½t£¬
”ßÅ×ĪļĻß £Øa£¾0£©æŖæŚĻņÉĻ£¬A£Ø1£¬2£©£¬M£¬N ŌŚøƶž“ĪŗÆŹżĶ¼ĻóÉĻ£¬ĒŅ5£¾2£¬
”ąÓɶž“ĪŗÆŹżµÄĶ¼Ļó¼°ŠŌÖŹµĆ£¬µćM£¬N·Ö±šĀäŌŚµćAµÄ×ó²ąŗĶÓŅ²ą£¬
”ąt©1£¼1£¼t+1£¬
”ątµÄȔֵ·¶Ī§ŹĒ0£¼t£¼2£»
£Ø3£©¢Ł²»ŹĒ£®·“ĄżČēĻĀ£ŗ
ČōÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½x2+1£¬Ōņ
°Ńy£½3x©1“śČėÉĻŹ½£¬µĆx2+1£½3x©1£¬
ÕūĄķµĆ£¬x2©3x+2£½0£¬
”ß”÷£½9©8£¾0£¬
”ą·½³Ģx2©3x+2£½0ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£¬
ŌņÅ×ĪļĻßy£½x2+1ÓėÖ±Ļßy£½3x©1ÓŠĮ½øö½»µć£¬
”ßy£½x2+1µÄ¶„µćĪŖ£Ø0£¬1£©
µ±x£½0Ź±£¬y£½3x©1£½©1£¼1£¬
”ąÅ×ĪļĻßy£½x2+1µÄ¶„µćŌŚÖ±Ļßy£½3x©1µÄÉĻ·½£¬
”ą“ĖÅ×ĪļĻߵĶ„µć²»ŌŚĶ¼ĻóCÉĻ£®
¢Ś”ßµćP¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖįµÄ¶Ō³ĘµćĪŖP”䣬ĒŅP”äŌŚĶ¼ĻóCÉĻ£¬
”ąµ±a£½1Ź±£¬øƶž“ĪŗÆŹży£½ax2+bx+c£Øa£¾0£©µÄĶ¼ĻóµÄ¶„µćŌŚÖ±Ļßy£½3x©1ĻĀ·½£¬
”ąµ±x£½©![]() Ź±£¬x2+bx+c£¼3x©1£¬
Ź±£¬x2+bx+c£¼3x©1£¬
¼“![]() £¬
£¬
°ŃA£Ø1£¬2£©“śČėy£½x2+bx+cÖŠ£¬µĆ1+b+c£½2£¬¹Źc£½1©b£¬
”ą![]() £¬
£¬
ÕūĄķµĆb2©2b£¾8£¬
”ą£Øb©1£©2£¾9£¬
”ąb©1£¾3»ņb©1£¼©3£¬
”ąb£¾4»ņb£¼©2£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćEŹĒÕż·½ŠĪABCDµÄ±ßBCŃÓ³¤ĻßÉĻŅ»µć£¬Į¬½įDE£¬¹ż¶„µćB×÷BF”ĶDE£¬“¹×ćĪŖF£¬BF·Ö±š½»ACÓŚH£¬½»BCÓŚG£® 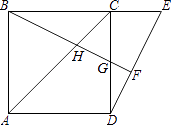
£Ø1£©ĒóÖ¤£ŗBG=DE£»
£Ø2£©ČōµćGĪŖCDµÄÖŠµć£¬Ēó ![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCµÄĆ껿ĪŖ3£¬BD£ŗDC£½2£ŗ1£¬EŹĒACµÄÖŠµć£¬ADÓėBEĻą½»ÓŚµćP£¬ÄĒĆ“ĖıߊĪPDCEµÄĆ껿ĪŖ£Ø””””£©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“Ó¼×µŲµ½ŅŅµŲÓŠ![]() ČżĢõ²»Ķ¬µÄ¹«½»ĻßĀ·£®ĪŖĮĖ½āŌēøß·åĘŚ¼äÕāČżĢõĻßĀ·ÉĻµÄ¹«½»³µ“Ó¼×µŲµ½ŅŅµŲµÄÓĆŹ±Ēéæö£¬ŌŚĆæĢõĻßĀ·ÉĻĖ껜єȔĮĖ500øö°ą“ĪµÄ¹«½»³µ£¬ŹÕ¼ÆĮĖÕāŠ©°ą“ĪµÄ¹«½»³µÓĆŹ±£Øµ„Ī»£ŗ·ÖÖÓ£©µÄŹż¾Ż£¬Ķ³¼ĘČēĻĀ£ŗ
ČżĢõ²»Ķ¬µÄ¹«½»ĻßĀ·£®ĪŖĮĖ½āŌēøß·åĘŚ¼äÕāČżĢõĻßĀ·ÉĻµÄ¹«½»³µ“Ó¼×µŲµ½ŅŅµŲµÄÓĆŹ±Ēéæö£¬ŌŚĆæĢõĻßĀ·ÉĻĖ껜єȔĮĖ500øö°ą“ĪµÄ¹«½»³µ£¬ŹÕ¼ÆĮĖÕāŠ©°ą“ĪµÄ¹«½»³µÓĆŹ±£Øµ„Ī»£ŗ·ÖÖÓ£©µÄŹż¾Ż£¬Ķ³¼ĘČēĻĀ£ŗ
¹«½»³µÓĆŹ±µÄʵŹż ¹«½»³µÓĆŹ±ĻßĀ· |
|
|
|
| ŗĻ¼Ę |
| 59 | 151 | 166 | 124 | 500 |
| 50 | 50 | 122 | 278 | 500 |
| 45 | 265 | 160 | 30 | 500 |
Ōēøß·åĘŚ¼ä£¬³Ė×ų_________£ØĢī”°![]() ”±£¬”°
”±£¬”°![]() ”±»ņ”°
”±»ņ”°![]() ”±£©ĻßĀ·ÉĻµÄ¹«½»³µ£¬“Ó¼×µŲµ½ŅŅµŲ”°ÓĆŹ±²»³¬¹ż45·ÖÖÓ”±µÄæÉÄÜŠŌ×ī“ó£®
”±£©ĻßĀ·ÉĻµÄ¹«½»³µ£¬“Ó¼×µŲµ½ŅŅµŲ”°ÓĆŹ±²»³¬¹ż45·ÖÖÓ”±µÄæÉÄÜŠŌ×ī“ó£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖÅ×ĪļĻßy=ax2+bx©5ÓėxÖį½»ÓŚA£Ø©1£¬0£©£¬B£Ø5£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£®
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČōµćDŹĒyÖįÉĻµÄŅ»µć£¬ĒŅŅŌB£¬C£¬DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬ĒóµćDµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£¬CE”ĪxÖįÓėÅ×ĪļĻßĻą½»ÓŚµćE£¬µćHŹĒÖ±ĻßCEĻĀ·½Å×ĪļĻßÉĻµÄ¶Æµć£¬¹żµćHĒŅÓėyÖįĘ½ŠŠµÄÖ±ĻßÓėBC£¬CE·Ö±š½»ÓŚµćF£¬G£¬ŹŌĢ½¾æµ±µćHŌĖ¶Æµ½ŗĪ“¦Ź±£¬ĖıߊĪCHEFµÄĆ껿×ī“ó£¬ĒóµćHµÄ×ų±ź¼°×ī“óĆ껿£»
£Ø4£©ČōµćKĪŖÅ×ĪļĻߵĶ„µć£¬µćM£Ø4£¬m£©ŹĒøĆÅ×ĪļĻßÉĻµÄŅ»µć£¬ŌŚxÖį£¬yÖįÉĻ·Ö±šÕŅµćP£¬Q£¬Ź¹ĖıߊĪPQKMµÄÖܳ¤×īŠ”£¬Ēó³öµćP£¬QµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠAB£½AC£¬”ĻBAC£½90”ć£¬·Ö±š¹żB”¢C×÷¹żAµćµÄÖ±Ļߵē¹Ļߣ¬“¹×ćĪŖD”¢E£®
£Ø1£©ĒóÖ¤£ŗ”÷AEC”Õ”÷BDA£»
£Ø2£©Čē¹ūCE£½2£¬BD£½4£¬ĒóEDµÄ³¤ŹĒ¶ąÉŁ£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABC ÖŠ£¬µć D ŹĒ±ß BC ÉĻµÄµć£ØÓė B”¢C Į½µć²»ÖŲŗĻ£©£¬¹żµć D×÷ DE”ĪAC£¬DF”ĪAB£¬·Ö±š½» AB”¢AC ÓŚ E”¢F Į½µć£¬ĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø £©
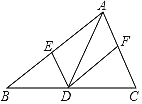
A. Čō AD Ę½·Ö”ĻBAC£¬ŌņĖıߊĪ AEDF ŹĒĮāŠĪ
B. Čō BD£½CD£¬ŌņĖıߊĪ AEDF ŹĒĮāŠĪ
C. Čō AD “¹Ö±Ę½·Ö BC£¬ŌņĖıߊĪ AEDF ŹĒ¾ŲŠĪ
D. Čō AD”ĶBC£¬ŌņĖıߊĪ AEDF ŹĒ¾ŲŠĪ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖAD”¢AE·Ö±šŹĒRt”÷ABCµÄøßŗĶÖŠĻߣ¬AB£½9cm£¬AC£½12cm£¬BC£½15cm£¬ŹŌĒó£ŗ
£Ø1£©ADµÄ³¤¶Č£»
£Ø2£©”÷ACEŗĶ”÷ABEµÄÖܳ¤µÄ²ī£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCŌŚÖ±½Ē×ų±źĻµÖŠ£¬
£Ø1£©ĒėŠ“³ö”÷ABCø÷µćµÄ×ų±ź£®
£Ø2£©Čō°Ń”÷ABCĻņÉĻĘ½ŅĘ2øöµ„Ī»£¬ŌŁĻņ×óĘ½ŅĘ1øöµ„Ī»µĆµ½”÷A”äB”äC”䣬Š“³ö A”䔢B”䔢C”äµÄ×ų±ź£¬²¢ŌŚĶ¼ÖŠ»³öĘ½ŅĘŗóĶ¼ŠĪ£®
£Ø3£©Ēó³öČż½ĒŠĪABCµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com