
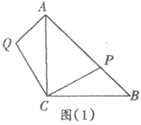
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
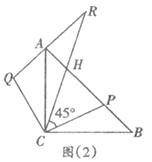
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.
【答案】(1)见解析;(2)①见解析;②见解析
【解析】
(1)依据AC=BC,可得∠CAB=∠B=45°,依据AQ⊥AB,可得∠QAC=∠CAB=45°=∠B,即可得到△ACQ≌△BCP;
(2)①依据△ACQ≌△BCP,则∠QCA=∠PCB,依据∠RCP=45°,即可得出∠QCR=45°=∠QAC,根据∠Q为公共角,可得△CQR∽△AQC,即可得到CQ2=QAQR;
②判定△QCH≌△PCH(SAS),即可得到HQ=HP,在Rt△QAH中,QA2+AH2=HQ2,依据QA=PB,即可得到AH2+PB2=HP2.
(1)∵AC=BC,
∴∠CAB=∠B=45°,
又∵AQ⊥AB,
∴∠QAC=∠CAB=45°=∠B,
在△ACQ和△BCP中,
 ,
,
∴△ACQ≌△BCP(SAS);
(2)①由(1)知△ACQ≌△BCP,则∠QCA=∠PCB,
∵∠RCP=45°,
∴∠ACR+∠PCB=45°,
∴∠ACR+∠QCA=45°,即∠QCR=45°=∠QAC,
又∠Q为公共角,
∴△CQR∽△AQC,
∴![]() ,
,
∴CQ2=QAQR;
②如图,连接QH,

由(1)(2)题知:∠QCH=∠PCH=45°,CQ=CP.
又∵CH是△QCH和△PCH的公共边,
∴△QCH≌△PCH(SAS).
∴HQ=HP,
∵在Rt△QAH中,QA2+AH2=HQ2,
又由(1)知:QA=PB,
∴![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直
,对称轴为直![]() .下列结论:
.下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 若点
若点![]() 点
点![]() 点
点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .其中正确的结论有( )
.其中正确的结论有( )
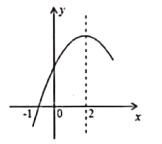
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
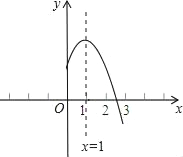
A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图像与性质,研究过程如下,请补充完整.
的图像与性质,研究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
| 10 |
| -2 | 1 |
| 1 | -2 | 3 | 10 |
|
其中,![]() _______,
_______,![]() =________;
=________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图像;

(3)观察函数图像:
①写出函数的一条图像性质:__________;
②当方程![]() 有且仅有两个不相等的实数根,根据函数图像直接写出
有且仅有两个不相等的实数根,根据函数图像直接写出![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线.
(2)若DE![]() ,∠C=30°,求
,∠C=30°,求![]() 的长.
的长.
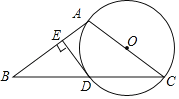
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(2,2),B(﹣1,a)
的图象交于点A(2,2),B(﹣1,a)
(1)求一次函数和反比例函数的表达式;
(2)设点P(h,y1),Q(h,y2)分别是两函数图象上的点;
①试直接写出当y1>y2时h的取值范围;
②若y1﹣y2=2,试求h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个四边形的一组对角互余,那么我们称这个四边形为“对角互余四边形”.
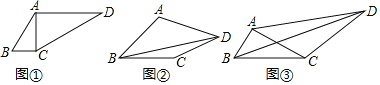
(1)如图①,在对角互余四边形ABCD中,∠B=60°,且AC⊥BC,AC⊥AD,若BC=1,则四边形ABCD的面积为 ;
(2)如图②,在对角互余四边形ABCD中,AB=BC,BD=13,∠ABC+∠ADC=90°,AD=8,CD=6,求四边形ABCD的面积;
(3)如图③,在△ABC中,BC=2AB,∠ABC=60°,以AC为边在△ABC异侧作△ACD,且∠ADC=30°,若BD=10,CD=6,求△ACD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com