
【题目】点![]() 在直线
在直线![]() 上,射线
上,射线![]() 在直线
在直线![]() 的上方,且
的上方,且![]()
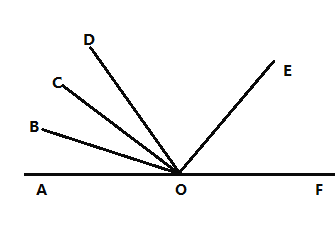
(1)如图1,![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]()
①若![]() =
=![]() ,则
,则![]() = .
= .
②若![]() =
=![]() ,则
,则![]() = .
= .
③若![]() =
=![]() ,则
,则![]() = °(用含
= °(用含![]() 的式子表示)
的式子表示)
(2)当![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]() 时,请画出图形;此时,
时,请画出图形;此时,![]() 与
与![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
【答案】(1)①40°;②25°;③(80-2n);(2)作图见详解;∠EOF=80°+2∠COD.
【解析】
(1)①由题意利用角平分线的定义和邻补角相加等于180°进行分析即可;
②根据题意设∠COD=x°,并利用角平分线的定义和邻补角相加等于180答题即可;
③根据题意可知需要利用角平分线的定义和邻补角相加等于180°来进行分析;
(2)根据题意画出新图形,并由题意用代数式分别表示∠COD与∠EOF,进而得出数量关系式.
解:(1)①∵∠AOB=40°,∠AOC=70°
∴∠BOC=30°
∵∠COD=20°
∴∠BOD=∠BOC+∠COD=50°
∵OD平分∠BOE
∴∠DOE=∠BOD=50°
∴∠EOF=180°-∠AOB-∠DOE-∠BOD=40°.
②设∠COD=x°,则由上题可知:
∠BOD=∠DOE=30°+x°
∴∠EOF=180°-(∠AOC+∠COD+∠DOE)=30°
∴∠COD=25°
③由上题可知:
∠BOD=∠DOE=30°+n°
∴∠EOF=180°-(∠AOC+∠COD+∠DOE)=180°-(70°+n°+30°+n°)=80°-2n°
故答案为①40°;②25°;③(80-2n).
(2)作图如下:

∠COD与∠EOF的数量关系是:∠EOF=80°+2∠COD,理由如下:
∵∠AOC=70°
∴∠COF=110°
∴∠EOF=∠EOC+110°
∵∠COD=∠EOC+∠DOE,①
∠DOE= ![]() ,
,
∴∠COD=15°+ ![]() ∠EOC,②
∠EOC,②
∴由①②得:∠EOF=80°+2∠COD.
答:∠COD与∠EOF的数量关系是:∠EOF=80°+2∠COD.


科目:初中数学 来源: 题型:
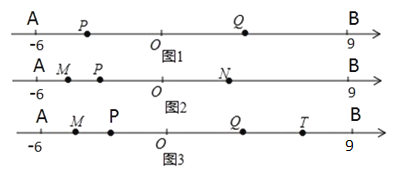
【题目】如图![]() ,已知在数轴上有
,已知在数轴上有![]() 、
、![]() 两点,点
两点,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() .点
.点![]() 在数轴上从点
在数轴上从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿数轴正方向运动,同时,点
个单位的速度沿数轴正方向运动,同时,点![]() 在数轴上从点
在数轴上从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度在沿数轴负方向运动,当点
个单位的速度在沿数轴负方向运动,当点![]() 到达点
到达点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() 秒.
秒.
(1)![]() _______;
_______;![]() 时,点
时,点![]() 表示的数是_______;当
表示的数是_______;当![]() _______时,
_______时,![]() 、
、![]() 两点相遇;
两点相遇;
(2)如图![]() ,若点
,若点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长;
的长;
(3)如图![]() ,若点
,若点![]() 为线段
为线段![]() 的中点.点
的中点.点![]() 为线段
为线段![]() 中点,则直接写出用含
中点,则直接写出用含![]() 的代数式表示的线段
的代数式表示的线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
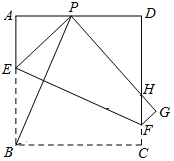
(1)求证:∠APB=∠BPH;
(2)若P为AD中点,求四边形EFGP的面积;
(3)当点P在边AD上移动时,△PDH的周长是否发生变化?写出你的结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
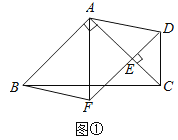
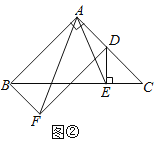
【题目】如图![]() ,在等腰
,在等腰![]() 中,
中,![]() ,点E在AC上
,点E在AC上![]() 且不与点A、C重合
且不与点A、C重合![]() ,在
,在![]() 的外部作等腰
的外部作等腰![]() ,使
,使![]() ,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
![]() 请直接写出线段AF,AE的数量关系;
请直接写出线段AF,AE的数量关系;
![]() 将
将![]() 绕点C逆时针旋转,当点E在线段BC上时,如图
绕点C逆时针旋转,当点E在线段BC上时,如图![]() ,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
![]() 若
若![]() ,
,![]() ,在图
,在图![]() 的基础上将
的基础上将![]() 绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正六边形ABCDEF的边长为![]() cm,点P为ABCDEF内的任意一点,点P到正六边形ABCDEF各边所在直线的距离之和为s,则s=_____cm.
cm,点P为ABCDEF内的任意一点,点P到正六边形ABCDEF各边所在直线的距离之和为s,则s=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
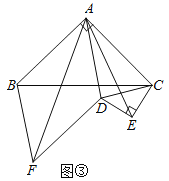
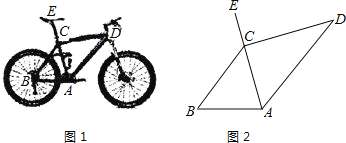
【题目】为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档CD与AD的长分别为60cm,75cm,且AC⊥CD,垂足为C,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AC的长;
(2)求车座点E到车架档AB的距离.
(结果精确到 1cm.参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75≈3.7321)
查看答案和解析>>
科目:初中数学 来源: 题型:
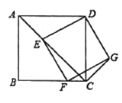
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
(1)如图,求证:矩形![]() 是正方形;
是正方形;
(2)当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,求
时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
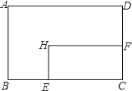
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A. 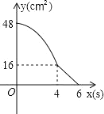 B.
B. 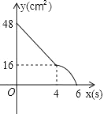 C.
C. 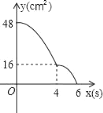 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=4,BC=8,D,E是AB和BC上的动点,连接CD,DE则CD+DE的最小值为( )

A. 8 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com