
如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的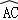 ,
,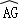 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.
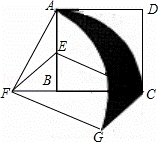
(1)证明:在正方形ABCD中,AB=BC=AD=2,∠ABC=90°,
∵△BEC绕点B逆时针旋转90°得到△ABF,
∴△ABF≌△CBE,
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=EC,
∴∠AFB+∠FAB=90°,
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,
∴∠CFG=∠FAB=∠ECB,
∴EC∥FG,
∵AF=EC,AF=FG,
∴EC=FG,
∴四边形EFGC是平行四边形,
∴EF∥CG;
(2)解:∵AD=2,E是AB的中点,
∴FE=BE= AB=
AB= ×2=1,
×2=1,
∴AF= =
= =
= ,
,
由平行四边形的性质,△FEC≌△CGF,
∴S△FEC=S△CGF,
∴S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG,
=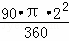 +
+ ×2×1+
×2×1+ ×(1+2)×1﹣
×(1+2)×1﹣ ,
,
=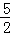 ﹣
﹣ .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为
A.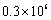
 B.
B.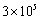 C.
C.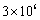 D.
D.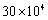
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年世界杯即将在巴西举行,根据预算巴西将总共花费14000000000美元,用于修建和翻新12个体育场,升级联邦、各州和各市的基础设施,以及为32支队伍和预计约60万名观众提供安保.将14000000000用科学记数法表示为( )
|
| A. | 140×108 | B. | 14.0×109 | C. | 1.4×1010 | D. | 1.4×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )

|
| A. | a2+4 | B. | 2a2+4a | C. | 3a2﹣4a﹣4 | D. | 4a2﹣a﹣2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
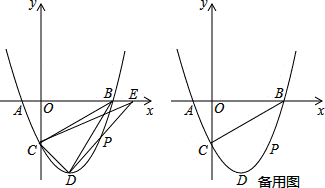
(1)求∠OBC的度数;
(2)连接CD、BD、DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com