
分析 先分别计算甲乙的平均数,再计算他们的方差,然后比较方差的大小判断谁的成绩稳定.
解答 解:甲的平均数=$\frac{1}{5}$(89+85+91+95+90)=90,
乙的平均数=$\frac{1}{5}$(98+82+80+95+95)=90,
甲的方差=$\frac{1}{5}$[(89-90)2+(85-90)2+(91-90)2+(95-90)2+(80-90)2]=10.4,
乙的方差=$\frac{1}{5}$[(98-90)2+(82-90)2+(80-90)2+(95-90)2+(95-90)2]=55.6,
因为甲的方差<乙的方差,
所以甲的成绩比较稳定.
故答案为甲.
点评 本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $2+\sqrt{2}=2\sqrt{2}$ | C. | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ | D. | $\frac{{\sqrt{12}+\sqrt{10}}}{2}=\sqrt{6}+\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
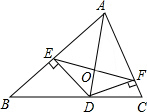 如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com