
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
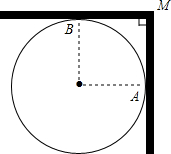 小红家的锅盖坏了,为了配一个锅盖,需要测量锅的直径(锅沿所形成的圆的直径),而小红家只有一把长20cm的直尺,根本不够长,怎么办呢?小红想了想,采取了以下办法:如图,首先把锅平放到墙根,锅沿刚好靠到两墙,用直尺紧贴墙面量得MA的长,即可求出锅的直径.请你利用图说明她这样做的理由.
小红家的锅盖坏了,为了配一个锅盖,需要测量锅的直径(锅沿所形成的圆的直径),而小红家只有一把长20cm的直尺,根本不够长,怎么办呢?小红想了想,采取了以下办法:如图,首先把锅平放到墙根,锅沿刚好靠到两墙,用直尺紧贴墙面量得MA的长,即可求出锅的直径.请你利用图说明她这样做的理由.查看答案和解析>>
科目:初中数学 来源: 题型:
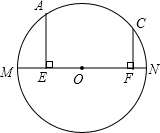 如图,MN=10是⊙O的直径,AE⊥MN于E,CF⊥MN于F,AE=4,CF=3,
如图,MN=10是⊙O的直径,AE⊥MN于E,CF⊥MN于F,AE=4,CF=3,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com