
���� ��1�����ݡ���Ϣ=��������ʡ�ʱ�䡱�����ʺ�ʱ��Ӧ��Ӧ����������ֵ�����㼴�ɵó����ۣ�
��2�����������ܵ�·��Ϊx�ף���ͬһ�ص��������ÿ������250�ף���ÿ������200�ף��ױ���������3���ӣ����з�����⣮
��3����ֱ��Ϊ0.4�ף���Ϊ3��Բ���λ���x����������������г����̲����
��� �⣺��1��������������ı���ΪxԪ����������ó���
x+3��4.25%x=33825��
���x=30000��
������������ı���Ϊ30000Ԫ��
��2�����������ܵ�·��Ϊx�ף�
����ʱ������з���Ϊ
$\frac{x}{250}$+3=$\frac{x}{200}$��
��֮�ã�x=3000
���������ܵ�·��3000�ף�
��3����ֱ��Ϊ0.4�ף���Ϊ3��Բ���λ���x����
������ã�[3����0.4��2��2��]x=[30����0.8��2��2�У�
���x=40��
����֪��Բ���θ����ɶ�����ֱ��Ϊ0.4�ף���Ϊ3��Բ���λ���40����
���� ������Ҫ������һԪһ�η��̵�Ӧ�ã��������⣬�ҵ����еĵ�����ϵ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCDΪ���Σ�����D���Խ���BD�Ĵ��ߣ���BC���ӳ����ڵ�E��ȡBE���е�F������DF��DF=4����AB=x��AD=y����x2+��y-4��2��ֵ��
��ͼ���ı���ABCDΪ���Σ�����D���Խ���BD�Ĵ��ߣ���BC���ӳ����ڵ�E��ȡBE���е�F������DF��DF=4����AB=x��AD=y����x2+��y-4��2��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=6cm��BC=8cm�������ζ��ۣ�ʹB����D���غϣ������ۺ�ΪEF����ͼ��EC�ij���
��ͼ������ABCD�У�AB=6cm��BC=8cm�������ζ��ۣ�ʹB����D���غϣ������ۺ�ΪEF����ͼ��EC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���������������У���A��B��C��M��N���ڸ���ϣ�
��ͼ���������������У���A��B��C��M��N���ڸ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
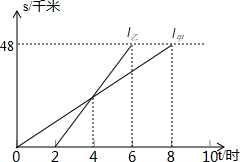 �ס������˵��������Σ��������г�������綯��������ͬ·��ǰ������ͼ��l����l���ֱ��ʾ�ס���ǰ��Ŀ�ĵ����ߵ�·��s/ǧ�������õ�ʱ��t/ʱ�Ĺ�ϵ��
�ס������˵��������Σ��������г�������綯��������ͬ·��ǰ������ͼ��l����l���ֱ��ʾ�ס���ǰ��Ŀ�ĵ����ߵ�·��s/ǧ�������õ�ʱ��t/ʱ�Ĺ�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������������һ�ø�7m����һ�ø�2m���������12m��һֻС���һ���������ң���A���ɵ���һ���������ң���C��������С�����ٷ��ж����ף�
��ͼ������������һ�ø�7m����һ�ø�2m���������12m��һֻС���һ���������ң���A���ɵ���һ���������ң���C��������С�����ٷ��ж����ף��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com