
·ЦОц ЈЁ1Ј©ПИ°Сёч¶юґОёщКЅ»ЇОЄЧојт¶юґОёщКЅЈ¬И»єуєПІўјґїЙЈ»
ЈЁ2Ј©ПИ°Сёч¶юґОёщКЅ»ЇОЄЧојт¶юґОёщКЅЈ¬И»єуЅшРР¶юґОёщКЅµДіэ·ЁФЛЛгЈ»
ЈЁ3Ј©ПИАыУГіЛ·Ё№«КЅХ№їЄЈ¬И»єуєПІўјґїЙЈ»
ЈЁ4Ј©°СxµДЦµґъИлґъКэКЅЦРЈ¬И»єуАыУГНкИ«ЖЅ·Ѕ№«КЅєНЖЅ·ЅІо№«КЅјЖЛгЈ®
Ѕвґр ЅвЈєЈЁ1Ј©ФКЅ=4$\sqrt{3}$-3$\sqrt{3}$+$\sqrt{3}$
=2$\sqrt{3}$Ј»
ЈЁ2Ј©ФКЅ=ЈЁ5$\sqrt{2}$-10$\sqrt{6}$Ј©ЎВ5$\sqrt{2}$
=1-2$\sqrt{3}$Ј»
ЈЁ3Ј©ФКЅ=12-4$\sqrt{6}$+2-ЈЁ$\sqrt{6}$+3+4+2$\sqrt{6}$Ј©
=14-4$\sqrt{6}$-3$\sqrt{6}$-7
=7-7$\sqrt{6}$Ј»
ЈЁ4Ј©µ±x=$\sqrt{3}$-1К±Ј¬ФКЅ=ЈЁ2+$\sqrt{3}$Ј©ЈЁ$\sqrt{3}$-1Ј©2-ЈЁ$\sqrt{3}$+1Ј©ЈЁ$\sqrt{3}$-1Ј©+7
=ЈЁ2+$\sqrt{3}$Ј©ЈЁ4-2$\sqrt{3}$Ј©-ЈЁ3-1Ј©+7
=2ЈЁ2+$\sqrt{3}$Ј©ЈЁ2-$\sqrt{3}$Ј©-2+7
=2ЈЁ4-3Ј©+5
=2+5
=7Ј®
µгЖА ±ѕМвїјІйБЛ¶юґОёщКЅµДјЖЛгЈєПИ°Сёч¶юґОёщКЅ»ЇОЄЧојт¶юґОёщКЅЈ¬ФЩЅшРР¶юґОёщКЅµДіЛіэФЛЛгЈ¬И»єуєПІўН¬Аа¶юґОёщКЅЈ®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
 РЎЕуґУѕµЧУЦРїґµЅЖыіµіµЕЖµДІї·ЦєЕВлИзНјЛщКѕЈ¬ФтёГіµЕЖХХµДІї·ЦєЕВлОЄE6395Ј®
РЎЕуґУѕµЧУЦРїґµЅЖыіµіµЕЖµДІї·ЦєЕВлИзНјЛщКѕЈ¬ФтёГіµЕЖХХµДІї·ЦєЕВлОЄE6395Ј®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
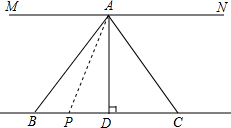 ТСЦЄЈєИзНјЈ¬ADЖЅ·ЦЎПBACЈ¬ЗТADЎНBCУЪµгDЈ¬MNЎОBCЈ¬ЗлФЪАЁєЕЦРІ№И«ІЅЦиµДНЖАнАнУЙЈ®
ТСЦЄЈєИзНјЈ¬ADЖЅ·ЦЎПBACЈ¬ЗТADЎНBCУЪµгDЈ¬MNЎОBCЈ¬ЗлФЪАЁєЕЦРІ№И«ІЅЦиµДНЖАнАнУЙЈ®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
| AЈ® | $\sqrt{2}$ЎБ$\sqrt{3}$=$\sqrt{6}$ | BЈ® | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | CЈ® | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | DЈ® | $\sqrt{ЈЁ-4Ј©^{2}}$=4 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
 ДіАдТыµгТ»МмКЫіцёчЦЦїЪО¶С©ёвКэБїµДЙИРОНіјЖНјИзНјЛщКѕЈ¬ЖдЦРКЫіцєм¶№їЪО¶µДС©ёв200Ц§Ј®
ДіАдТыµгТ»МмКЫіцёчЦЦїЪО¶С©ёвКэБїµДЙИРОНіјЖНјИзНјЛщКѕЈ¬ЖдЦРКЫіцєм¶№їЪО¶µДС©ёв200Ц§Ј®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
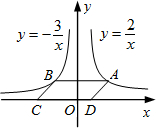 ИзНјЈ¬µгAКЗ·ґ±ИАэєЇКэy=$\frac{2}{x}$ЈЁxЈѕ0Ј©µДНјПуЙПИОТвТ»µгЈ¬ABЎОxЦбІў·ґ±ИАэєЇКэy=-$\frac{3}{x}$µДНјПуУЪµгBЈ¬ТФABОЄ±ЯЧч?ABCDЈ¬ЖдЦРµгCЈ¬DФЪxЦбЙПЈ¬Фт?ABCDµДГж»эОЄЈЁЎЎЎЎЈ©
ИзНјЈ¬µгAКЗ·ґ±ИАэєЇКэy=$\frac{2}{x}$ЈЁxЈѕ0Ј©µДНјПуЙПИОТвТ»µгЈ¬ABЎОxЦбІў·ґ±ИАэєЇКэy=-$\frac{3}{x}$µДНјПуУЪµгBЈ¬ТФABОЄ±ЯЧч?ABCDЈ¬ЖдЦРµгCЈ¬DФЪxЦбЙПЈ¬Фт?ABCDµДГж»эОЄЈЁЎЎЎЎЈ©| AЈ® | 3 | BЈ® | 5 | CЈ® | 7 | DЈ® | 9 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
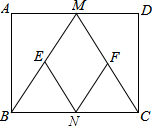 ИзНјЈ¬ФЪѕШРОABCDЦРЈ¬MЎўN·Ц±рКЗ±ЯADЎўBCµДЦРµгЈ¬EЎўF·Ц±рКЗ±ЯBMЎўCMµДЦРµгЈ¬µ±ABЈєAD=1Јє2К±Ј¬ЛД±ЯРОMENFКЗХэ·ЅРОЈ®
ИзНјЈ¬ФЪѕШРОABCDЦРЈ¬MЎўN·Ц±рКЗ±ЯADЎўBCµДЦРµгЈ¬EЎўF·Ц±рКЗ±ЯBMЎўCMµДЦРµгЈ¬µ±ABЈєAD=1Јє2К±Ј¬ЛД±ЯРОMENFКЗХэ·ЅРОЈ®Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com