Question

用因式分解法解方程

(1)

(2)

(3)t(2t－1)=3(2t－1)

(4)(2x－1)(x－1)=1

Answer 1

答案：略
解析：

解：(1)原方程可变形为(x＋5)(x－3)=0， 得x＋5=0或x－3=0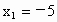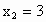． ∴，． (2)方程可变形为(y＋1)(y＋6)=0， 得y＋1=0或y＋6=0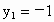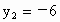， ∴，， (3)方程可变形为t(2t－1)－3(2t－1)=0， 得(2t－1)(t－3)=0， 于是2t－1=0或t－3=0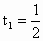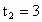， ∴，． (4)方程可变形为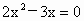． x(2x－3)=0， x=0或2x－3=0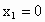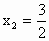． ∴，． 应用因式分解法解形如(x－a)(x－b)=c的方程时，其左边是两个一次因式之积，但右边不是零，应转化为形如(x－e)(x－f)=0的形式，这时才有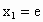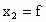，否则会产生错误，如(4)可能产生如下的错解： 原方程变形为：2x－1=1或x－1=1．∴，．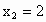

提示：

在用因式分解法解一元二次方程时，一般地要把方程整理为一般式，如果左边的代数式能够分解为两个一次因式的乘积，而右边为零时，则可令每一个一次因式为零，得到两个一元一次方程，解出这两个一元一次方程的解就是原方程的两个解．注意在方程(3)中，方程两边不能同除以(2t－1)．