练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．下列四个命题中
    ①一组对边平行且相等的四边形是平行四边形；②一组邻边相等的平行四边形是正方形；
    ③对角线相等的四边形是矩形；           ④对角线互相垂直平分的四边形是菱形
    正确命题的序号是（　　）
    A．①②B．②③C．③④D．①④

    分析 根据平行四边形、正方形、矩形、菱形的判定方法，针对每一个命题进行分析，即可选出答案．

    解答 解：①一组对边平行且相等的四边形是平行四边形，是真命题；
    ②一组邻边相等的矩形是正方形，是假命题；
    ③对角线相等的平行四边形是矩形，是假命题；          
    ④对角线互相垂直平分的四边形是菱形，是真命题．
    故选D．

    点评 主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．本题关键是要熟练掌握平行四边形、正方形、矩形、菱形的判定方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．用乘法公式计算
    （1）20012-2000×2002
    （2）1982．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）数学爱好者小森偶然阅读到这样一道竞赛题：
    一个圆内接六边形ABCDEF，各边长度依次为 3，3，3，5，5，5，求六边形ABCDEF的面积．
    小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理，将六边形进行分割重组，得到图③．可以求出六边形ABCDEF的面积等于$\frac{47\sqrt{3}}{4}$．

    （2）类比探究：一个圆内接八边形，各边长度依次为2，2，2，2，3，3，3，3．求这个八边形的面积．
    请你仿照小森的思考方式，求出这个八边形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

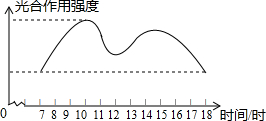    11．光合作用是指绿色植物通过叶绿体，利用光能，把二氧化碳和水转化成储存能量的有机物，并释放出氧气的过程．如图是夏季的白天7时～18时的一般的绿色植物的光合作用强度与时间之间的关系的曲线，分析图象回答问题：观察：
    （1）大约几时的光合作用最强？
    （2）大约几时的光合作用最弱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．不等式x2+ax+b≥0（a≠0）的解集为全体实数，假设f（x）=x2+ax+b，若关于x的不等式f（x）＜c的解集为（m，m+6），则实数c的值为9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．有下列四个命题：①3是9的一个平方根②实数和数轴上的点是一一对应的．③在同一平面内，两条直线的位置关系有两种：相交和平行；④$\root{3}{7}$的整数部分是2，小数部分是2-$\root{3}{7}$．其中假命题有（填序号）①②③．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

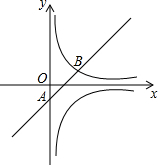    15．如图，已知直线l经过点A（0，-1），与双曲线y=$\frac{m}{x}$（x＞0）交于点B（2，1）．点P在线段AB上，过点P作x轴的垂线分别交双曲线y=$\frac{m}{x}$（x＞0）和y=-$\frac{m}{x}$（x＞0）于点M、N．
    （1）求m的值和直线l的解析式；
    （2）求S△AMN；
    （3）是否存在点P，使得S△AMP=$\frac{1}{4}$S△AMN？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

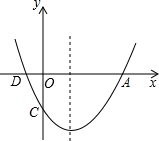    12．如图，二次函数y=ax2+bx+c的图象与x轴的交点为A、D（A在D的右侧），与y轴的交点为C，且A（4，0）．C（0，-3），对称轴是直线x=l．
    （1）求二次函数的解析式；
    （2）若M是第四象限抛物线上一动点，且横坐标为m，设四边形OCMA的面积为s．请写出s与m之间的函数关系式，并求出当m为何值时，四边形OCMA的面积最大；
    （3）设点B是x轴上的点，P是抛物线上的点，是否存在点P，使得以A，B、C，P四点为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱①③④（写出所有正确结果的序号）．

    查看答案和解析>>

    同步练习册答案