
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出以下顶点的坐标:A( , );B( , ) ;C( , ).
(2)顶点A关于x轴对称的点A′的坐标( , ),顶点C关于y轴对称的点C′的坐标( , ).
(3)求△ABC的面积.
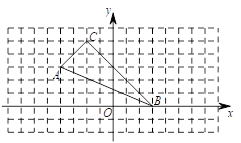
【答案】⑴A(-4,3),B(3,0),C(-2,5);⑵A,(-4,-3),C,(2,5);⑶10.
【解析】
(1)根据平面直角坐标系即可求得答案.
(2)根据点关于x轴对称的特征:横坐标相同,纵坐标互为相反数;点关于y轴对称的特征:横坐标互为相反数,纵坐标不变;依次即可得出答案.
(3)将图中△ABC分割成一个长方形减去三个三角形的面积即可得出答案.
(1)分别写出△ABC各个顶点的坐标:A(-4,3),B(3,0),C(-2,5).
(2)顶点A关于x轴对称的点A′的坐标(-4,-3),顶点C关于y轴对称的点C′的坐标(2,5).
(3)如图:
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]()
=![]()
=![]()
=![]()
故△ABC的面积为10.


科目:初中数学 来源: 题型:
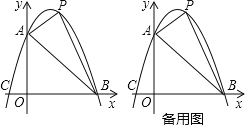
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.

已知:如图,钝角∠AOB.求作:∠AOB的角平分线.
作法:

①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() 的长为半径作弧,在∠AOB内,两弧交于点C;
的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
在该作图中蕴含着几何的证明过程:
由①可得:OD=OE
由②可得:_________________
由③可知:OC=OC
∴______≌_________(依据:________________________)
∴可得∠COD=∠COE(全等三角形对应角相等)
即OC就是所求作的∠AOB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
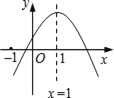
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0②9a+c>3b;③8a+7b+2c>0④若点A(﹣3,y1),点B(﹣2,y2),点C(8,y3)在该函数图象上,则y1<y3<y2⑤若方程a(x﹣1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣l<5<x2,其中正确的结论有( )
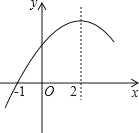
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()
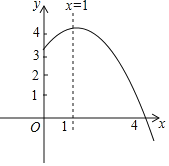
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】师徒二人各加工同样多的零件,师父每小时加工200个,徒弟每小时加工125个.若徒弟先加工段时间之后,师父才开始工作师父工作2小时后发现自己加工的零件个数和徒弟加工的个数刚好相同,如图是师徒两人完成的零件个数之差y(个)与徒弟工作的时间x(小时)之间的函数图象,根据图象回答问题:
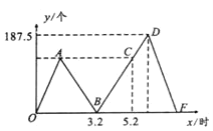
(1)求出点A的坐标,并解释该点坐标表示的实际意义;
(2)求出线段BD的函数表达式;
(3)求徒弟这次加工的零件总数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )
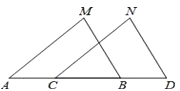
A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com