练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知x-$\frac{1}{x}$=7，则x2+$\frac{1}{{x}^{2}}$=51．

    分析 直接利用完全平方公式将已知条件变形求出即可．

    解答 解：∵x-$\frac{1}{x}$=7，
    ∴（x-$\frac{1}{x}$）2=49，
    ∴x2+$\frac{1}{{x}^{2}}$=51．
    故答案为：51．

    点评 此题主要考查了完全平方公式，正确应用完全平方公式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    3．减-3x等于5x2-3x-5的多项式为5x2-6x-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．计算：a2•（-a）3的结果正确的是（　　）
    A．-a5B．a5C．-a6D．a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．求下列各式中的x
    ①（x-1）3=-8
    ②（x+1）2=25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．若点P（m，n）在第二象限，则点Q（m，-n）在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列说法错误的是（　　）
    A．一组数据的平均数、众数、中位数可能是同一个数
    B．一组数据中中位数可能不唯一确定
    C．一组数据中平均数、众数、中位数是从不同角度描述了一组数据的集中趋势
    D．一组数据中众数可能有多个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列运算正确的是（　　）
    A．$（3-2\sqrt{3}）（3+2\sqrt{3}）={3^2}$-2×3=3B．$（2\sqrt{a}+\sqrt{b}）（\sqrt{a}-\sqrt{b}）=2a-b$
    C．${（3-2\sqrt{3}）^2}={3^2}-{（2\sqrt{3}）^2}$=9-12=-3D．$（\sqrt{a}+\sqrt{a-1}）（\sqrt{a}-\sqrt{a-1}）={（\sqrt{a}）^2}-{（\sqrt{a-1}）^2}$=a-（a-1）=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）（3-π）0-$\sqrt{2}$cos45°+（$\frac{1}{2}$）-1-|-4|
    （2）4sin60°+（-2）-1-（$\sqrt{2009}$-2008）0
    （3）tan260°+4sin30°•cos45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

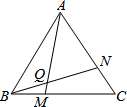    8．如图，已知△ABC中，AB=BC=AC，∠ABC=∠BCA=∠CAB=60°，M、N分别在△ABC的BC、AC边上，且BM=CN，AM、BN交于点Q．求证：∠BQM=60°．
    （1）请你完成这道思考题；
    （2）做完（1）后，同学们在老师的启发下进行了反思，提出了许多问题，如：
    ①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？
    ②若将题中的点M、N分别移动到BC、CA的延长线上，是否仍能得到∠BQM=60°？
    请你作出判断，在下列横线上填写“是”或“否”：①是；②是．

    查看答案和解析>>

    同步练习册答案