
 如图,点A的坐标为(-1,0),点B(a,-2)在直线y=2x-4上.
如图,点A的坐标为(-1,0),点B(a,-2)在直线y=2x-4上.分析 (1)将点B(a,-2)代入y=2x-4,即可求出a的值;设直线AB的解析式为y=kx+b,将点A、点B的坐标代入,运用待定系数法求出直线AB的解析式为y=-x-1;
(2)根据平移的规律得出把直线AB向上平移m个单位后的解析式y=-x+m-1,然后解方程组$\left\{\begin{array}{l}{y=-x+m-1}\\{y=2x-4}\end{array}\right.$,求出交点坐标为($\frac{m+3}{3}$,$\frac{2m-6}{3}$),然后根据第一象限内点的坐标特征列出不等式组$\left\{\begin{array}{l}{\frac{m+3}{3}>0}\\{\frac{2m-6}{3}>0}\end{array}\right.$,解不等式组即可.
解答 解:(1)∵点B(a,-2)在直线y=2x-4上,
∴2a-4=-2,
解得a=1;
设直线AB的解析式为y=kx+b.
∵点A的坐标为(-1,0),点B的坐标是(1,-2),
∴$\left\{\begin{array}{l}{-k+b=0}\\{k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴直线AB的解析式为y=-x-1;
(2)把直线AB向上平移m个单位后得y=-x+m-1.
由$\left\{\begin{array}{l}{y=-x+m-1}\\{y=2x-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{m+3}{3}}\\{y=\frac{2m-6}{3}}\end{array}\right.$,
即交点为($\frac{m+3}{3}$,$\frac{2m-6}{3}$).
由题意,得$\left\{\begin{array}{l}{\frac{m+3}{3}>0}\\{\frac{2m-6}{3}>0}\end{array}\right.$,
解得m>3.
点评 本题考查了一次函数图象与几何变换,运用待定系数法求直线的解析式,一次函数图象上点的坐标特征,两函数交点坐标的求法,直线平移的规律等知识,综合性较强,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,有一个面积是120平方米的长方形养鸡场,鸡场的一边靠墙,墙长16米,与墙垂直的两侧均有一个1米宽的小门,除门外都用竹篱笆围成.若竹篱笆的总长30米,则鸡场的两邻边长各是多少?
如图,有一个面积是120平方米的长方形养鸡场,鸡场的一边靠墙,墙长16米,与墙垂直的两侧均有一个1米宽的小门,除门外都用竹篱笆围成.若竹篱笆的总长30米,则鸡场的两邻边长各是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
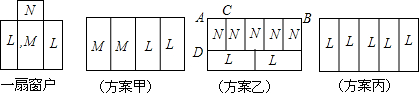
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com