
 Ćė£¬ĒėĒó³ö”÷APQµÄĆ껿SÓėtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öµ±tĪŖŗĪÖµŹ±£¬”÷APQµÄĆ껿×ī“ó£¬×ī“óĆ껿ŹĒ¶ąÉŁ£æ
Ćė£¬ĒėĒó³ö”÷APQµÄĆ껿SÓėtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öµ±tĪŖŗĪÖµŹ±£¬”÷APQµÄĆ껿×ī“ó£¬×ī“óĆ껿ŹĒ¶ąÉŁ£æ | 1 |
| 2 |
| 2 |
|
|
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 26”¢ŅŃÖŖ£ŗČēĶ¼£¬Å×ĪļĻßC1£¬C2¹ŲÓŚxÖį¶Ō³Ę£»Å×ĪļĻßC1£¬C3¹ŲÓŚyÖį¶Ō³Ę£®Å×ĪļĻßC1£¬C2£¬C3ÓėxÖįĻą½»ÓŚA”¢B”¢C”¢DĖÄµć£»ÓėyĻą½»ÓŚE”¢FĮ½µć£»H”¢G”¢M·Ö±šĪŖÅ×ĪļĻßC1£¬C2£¬C3µÄ¶„µć£®HN“¹Ö±ÓŚxÖį£¬“¹×ćĪŖN£¬ĒŅ|OE|£¾|HN|£¬|AB|”Ł|HG|
26”¢ŅŃÖŖ£ŗČēĶ¼£¬Å×ĪļĻßC1£¬C2¹ŲÓŚxÖį¶Ō³Ę£»Å×ĪļĻßC1£¬C3¹ŲÓŚyÖį¶Ō³Ę£®Å×ĪļĻßC1£¬C2£¬C3ÓėxÖįĻą½»ÓŚA”¢B”¢C”¢DĖÄµć£»ÓėyĻą½»ÓŚE”¢FĮ½µć£»H”¢G”¢M·Ö±šĪŖÅ×ĪļĻßC1£¬C2£¬C3µÄ¶„µć£®HN“¹Ö±ÓŚxÖį£¬“¹×ćĪŖN£¬ĒŅ|OE|£¾|HN|£¬|AB|”Ł|HG|²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
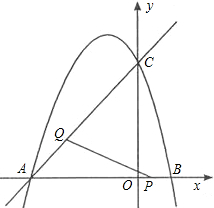
 ČēĶ¼£¬Å×ĪļĻß½»xÖįÓŚµćA£Ø-2£¬0£©£¬µćB£Ø4£¬0£©£¬½»yÖįÓŚµćC£Ø0£¬4£©£®
ČēĶ¼£¬Å×ĪļĻß½»xÖįÓŚµćA£Ø-2£¬0£©£¬µćB£Ø4£¬0£©£¬½»yÖįÓŚµćC£Ø0£¬4£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ŅŌPĪŖŌ²ŠÄµÄŌ²¾¹żµćA£¬²¢ĒŅÓėÖ±ĻßBMĻąĒŠ£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
ŅŌPĪŖŌ²ŠÄµÄŌ²¾¹żµćA£¬²¢ĒŅÓėÖ±ĻßBMĻąĒŠ£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 £®µćCŹĒµćA¹ŲÓŚµćBµÄ¶Ō³Ęµć£¬µćFŹĒĻ߶ĪBCµÄÖŠµć£¬Ö±Ļßl¹żµćFĒŅÓėyÖįĘ½ŠŠ£®Ö±Ļßy=-x+m¹żµćC£¬½»yÖįÓŚDµć£®
£®µćCŹĒµćA¹ŲÓŚµćBµÄ¶Ō³Ęµć£¬µćFŹĒĻ߶ĪBCµÄÖŠµć£¬Ö±Ļßl¹żµćFĒŅÓėyÖįĘ½ŠŠ£®Ö±Ļßy=-x+m¹żµćC£¬½»yÖįÓŚDµć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬Å×ĪļĻßy=ax2+bx+c£Øa”Ł0£©ÓėxÖįĮ½½»µćŹĒA£Ø-1£¬0£©£¬B£Ø3£¬0£©£¬ŌņČēĶ¼æÉÖŖy£¼0Ź±£¬xµÄȔֵ·¶Ī§ŹĒ£Ø””””£©
ČēĶ¼£¬Å×ĪļĻßy=ax2+bx+c£Øa”Ł0£©ÓėxÖįĮ½½»µćŹĒA£Ø-1£¬0£©£¬B£Ø3£¬0£©£¬ŌņČēĶ¼æÉÖŖy£¼0Ź±£¬xµÄȔֵ·¶Ī§ŹĒ£Ø””””£©| A”¢-1£¼x£¼3 | B”¢3£¼x£¼-1 | C”¢x£¾-1»ņx£¼3 | D”¢x£¼-1»ņx£¾3 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com