
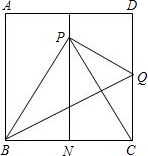
 如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC.
如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC.| ∥ |
. |
| 1 |
| 2 |
| 1 |
| 2 |
| ∥ |
. |

| 1 |
| 2 |
| PC2-NC2 |
| 3 |
| 3 |


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
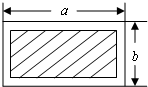 25、如图,有一块长为a米、宽为b米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
25、如图,有一块长为a米、宽为b米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.
如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
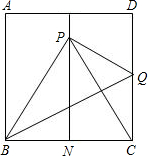 如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC.
如图,有一块面积为4的正方形ABCD,M、N分别为AD、BC边上的中点,将C点折至MN上,落在P点位置,折痕为BQ,连接PQ、PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.
如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com