
 ��ͼ���ڡ�ABC�У�ADƽ�֡�BAC��DF��AB��DM��AC��AB=18cm��AF=12cm��AC=16cm������E��2cm/s���ٶȴ�A����F���˶�������G��1cm/s���ٶȴ�C����A���˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶������˶�ʱ��Ϊt��
��ͼ���ڡ�ABC�У�ADƽ�֡�BAC��DF��AB��DM��AC��AB=18cm��AF=12cm��AC=16cm������E��2cm/s���ٶȴ�A����F���˶�������G��1cm/s���ٶȴ�C����A���˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶������˶�ʱ��Ϊt������ ��1�����ݽ�ƽ���ߵ����ʣ��ó�DF=DM���ٸ���S��ABD=$\frac{1}{2}$��AB��DF��S��ACD=$\frac{1}{2}$��AC��DM�����ɵó�$\frac{{S}_{��ABD}}{{S}_{��ACD}}$��ֵ��
��2�����ݶ���E��2cm/s���ٶȴ�A����F���˶�������G��1cm/s���ٶȴ�C����A���˶����ɵ�AE=2t��CG=t����DF=DM���ٸ���$\frac{{S}_{��AED}}{{S}_{��DGC}}$=$\frac{\frac{1}{2}AE•DF}{\frac{1}{2}CG•DM}$���м�����⼴�ɣ�
��3������������������ۣ��ٵ���G���߶�CM��ʱ���ڵ���G���߶�MA��ʱ���ֱ���ݡ�DFE�ա�DMG���ó�EF=GM���ݴ��г�����t�ķ��̣�������⼴�ɣ�
��� �⣺��1����ADƽ�֡�BAC��DF��AB��DM��AC
��DF=DM��
�֡�S��ABD=$\frac{1}{2}$��AB��DF��S��ACD=$\frac{1}{2}$��AC��DM��
��$\frac{{S}_{��ABD}}{{S}_{��ACD}}$=$\frac{AB}{AC}$=$\frac{18}{16}$=$\frac{9}{8}$��
��2��֤�����߶���E��2cm/s���ٶȴ�A����F���˶�������G��1cm/s���ٶȴ�C����A���˶���
��AE=2t��CG=t����DF=DM��
��$\frac{{S}_{��AED}}{{S}_{��DGC}}$=$\frac{\frac{1}{2}AE•DF}{\frac{1}{2}CG•DM}$=$\frac{AE}{CG}$=$\frac{2t}{t}$=2��
��3������ͼ1������G���߶�CM��ʱ��
EF=AF-AE=12-2t��AM=AF=12��GM=CM-CG=��16-12��-t=4-t��
�ߡ�DFE�ա�DMG��
��EF=GM��
��12-2t=4-t��
��t=8����ȥ����
����ͼ2������G���߶�MA��ʱ��
EF=AF-AE=12-2t��GM=CG-CM=t-4��
�ߡ�DFE�ա�DMG��
��EF=GM��
��12-2t=t-4��
��t=$\frac{16}{3}$��
����������t=$\frac{16}{3}$��
���� ���������������ۺ��⣬��Ҫ�����˽�ƽ���ߵ����ʣ�ȫ�������ε����ʣ������ε���������Լ���һԪһ�η��̵����ã��������Ĺؼ������գ��ǵ�ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȣ�����ʱע������ȫ�������εĶ�Ӧ������г����̣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���ĸ�ȫ�ȵ�ֱ��������ƴ����һ����ͼ��ʾ��ͼ�Σ�����a��ʾ�϶�ֱ�DZߣ�b��ʾ�ϳ���ֱ�DZߣ�c��ʾб�ߣ����������ͼ��֤�����ɶ�����
���ĸ�ȫ�ȵ�ֱ��������ƴ����һ����ͼ��ʾ��ͼ�Σ�����a��ʾ�϶�ֱ�DZߣ�b��ʾ�ϳ���ֱ�DZߣ�c��ʾб�ߣ����������ͼ��֤�����ɶ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �������֤�����̣�
�������֤�����̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�Ȳ���������Ҳ���Ǹ���������0���������� | |
| B�� | ��-3��-1֮�����һ�������� | |
| C�� | һ�������ĵ���һ�����Ǹ��� | |
| D�� | һ�����ľ���ֵԽ��ʾ���ĵ���������Խ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
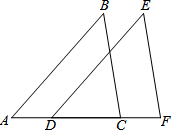
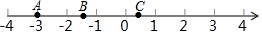 ��ͼ��ʾ����������A��B��C�����㣬�ҵ�B���߶�AC���е㣬��A��ʾ-3����B��ʾ����-$\sqrt{2}$�����C��ʾ������-2$\sqrt{2}$+3��
��ͼ��ʾ����������A��B��C�����㣬�ҵ�B���߶�AC���е㣬��A��ʾ-3����B��ʾ����-$\sqrt{2}$�����C��ʾ������-2$\sqrt{2}$+3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ʵ��a��b�������Ӧ���λ����ͼʾ���������½��ۣ���a��-2����a��-3����a��-b����-a��-b����a-b��0����|a|��b����|a|-b��1����|a-1|��b����a+2b��0��������ȷ�Ľ����Ǣۢݢޢ�ᣨ��д��ţ�
ʵ��a��b�������Ӧ���λ����ͼʾ���������½��ۣ���a��-2����a��-3����a��-b����-a��-b����a-b��0����|a|��b����|a|-b��1����|a-1|��b����a+2b��0��������ȷ�Ľ����Ǣۢݢޢ�ᣨ��д��ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
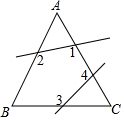 ��ͼ��ʾ���ڵȱ�������ABC�У���ȥ��A����C��1+��2+��3+��4=480�㣮
��ͼ��ʾ���ڵȱ�������ABC�У���ȥ��A����C��1+��2+��3+��4=480�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com