
【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与C重合,折痕EF交AD于E,交BC于F,交AC于O,连结AF、CE. 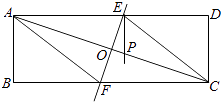
(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:AE2=AOAP;
(3)若AE=8,△ABF的面积为9,求AB+BF的值.
【答案】
(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO
∴△AOE≌△COF(AAS)
∴OE=OF
∴四边形AFCE是菱形
(2)证明:∵EP⊥AD
∴∠AEP=90°,
∵∠AOE=90°,
∴∠AEP=∠AOE
∵∠EAO=∠EAP
∴△AOE∽△AEP
∴ ![]()
∴AE2=AOAP
(3)解:∵四边形AFCE是菱形
∴AF=AE=8
在Rt△ABF中,AB2+BF2=AF2
∴AB2+BF2=82
∴(AB+BF)2﹣2ABBF=64①
∵△ABF的面积为9
∴ ![]()
∴ABBF=18②
由①、②得:(AB+BF)2=100
∵AB+BF>0
∴AB+BF=10
【解析】(1)当顶点A与C重合时,折痕EF垂直平分AC,由OA=OC,得∠AOE=∠COF=90°,由题意得AD∥BC,∠EAO=∠FCO,可证明△AOE≌△COF,从而得出∴四边形AFCE是菱形. (2)由EP⊥AD,得∠AEP=90°,可证明△AOE∽△AEP,写出比例式 ![]() ,即可得出AE2=AOAP;(3)根据四边形AFCE是菱形,得出AF=AE=8,在Rt△ABF中,利用勾股定理得AB2+BF2=AF2 , AB2+BF2=82 , 即可得出(AB+BF)2﹣2ABBF=64①,根据△ABF的面积为9,可求得ABBF=18②,再由①、②得:(AB+BF)2=100,得出AB+BF=10.
,即可得出AE2=AOAP;(3)根据四边形AFCE是菱形,得出AF=AE=8,在Rt△ABF中,利用勾股定理得AB2+BF2=AF2 , AB2+BF2=82 , 即可得出(AB+BF)2﹣2ABBF=64①,根据△ABF的面积为9,可求得ABBF=18②,再由①、②得:(AB+BF)2=100,得出AB+BF=10.
【考点精析】掌握勾股定理的概念和矩形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM= , CM= . 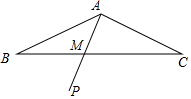
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
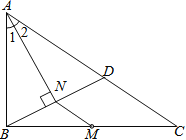
(1)求证:BN=DN;
(2)求△ABC的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y= ![]() x2+1(如图所示).
x2+1(如图所示).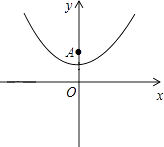
(1)填空:抛物线的顶点坐标是( , ),对称轴是;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE. 
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD= ![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线: 作法:如图,
⑴在射线OA上任取一点C,过点C作CD∥OB;
⑵以点C为圆心,CO的长为半径作弧,交CD于点E;
⑶作射线OE.
所以射线OE就是∠AOB的角平分线.请回答:小米的作图依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com