
【题目】某超市拟购进甲乙两种大米,购进计划见下表:
品种 项目 | 数量 (单位:kg) | 进价 (单位:元/kg) | 售价的设定标准 |
甲种大米 | 600 | a | 在进价的基础上提高40% |
乙种大米 | 800 | b | 在进价的基础上提高30% |
(1)若计划购进的大米全部售出,超市可获利多少元?(用含有a,b的代数式表示结果)
(2)由于包装袋破损,两种大米混合在一起,无法分装,超市决定以散装米出售,售价为![]() 元/kg,若这批大米全部售出,超市是赚钱还是亏本,请说明理由?
元/kg,若这批大米全部售出,超市是赚钱还是亏本,请说明理由?
 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】据《南昌晚报》2019 年 4 月 28 日报道,“五一”期间南昌天气预报气温如下:
时间 | 4 月 29 日 | 4 月 30 日 | 5 月 1 日 | 5 月 2 日 | 5 月 3 日 |
最低气温 | 18℃ | 18℃ | 19℃ | 18℃ | 19℃ |
最高气温 | 22℃ | 24℃ | 27℃ | 22℃ | 24℃ |
则“五一”期间南昌天气预报气温日温差最大的时间是( )
A. 4 月 29 日B. 4 月 30 日C. 5 月 1 日D. 5 月 3 日
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,人们对健康愈加重视,跑步锻炼成了人们的首要选择,许多与运动有关的手机APP应运而生,聪聪给自己定了目标,每天跑步![]() 公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
日期 | 18日 | 19日 | 20日 | 21日 | 22日 | 23日 | 24日 |
路程(公里) | +1.72 | +3.20 | —1.91 | —0.96 | —1.88 | +3.30 | +0.07 |
(1)分别用含![]() 的代数式表示22日及23日的跑步路程;
的代数式表示22日及23日的跑步路程;
(2)如图所示是聪聪24日跑步路程是7.07公里,求![]() 的值;
的值;
(3)若跑步一公里消耗的热量为60千卡,请问聪聪跑步七天一共消耗了多少热量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四个结论中正确的是_____(填写序号).
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1;
④如果5是方程M的一个根,那么![]() 是方程N的一个根.
是方程N的一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=_____.
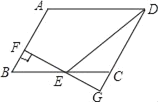
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
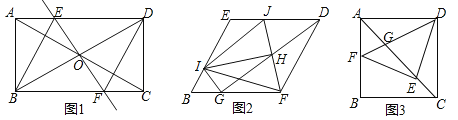
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
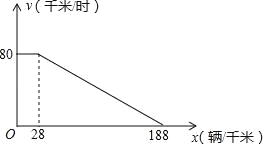
【题目】“城市发展 交通先行”,成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程,建成后将大大提升二环路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示.
(1)求当28<x≤188时,V关于x的函数表达式;
(2)若车流速度V不低于50千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点 O 是坐标原点,四边形 ABCO 是菱形,点 A 的坐标为(-3,4),点 C 在 x 轴的正半轴上,直线 AC 交 y 轴于点 M,AB 边交 y 轴于点 H.
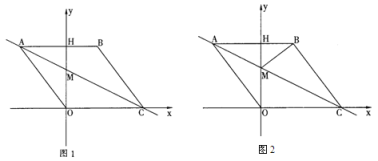
(1)求直线 AC 的解析式;
(2)连接 BM,如图 2,动点 P 从点 A 出发,沿折线 ABC 方向以 2 个单位/秒的速度向终点 C 匀速运动,设△PMB 的面积为 S(S≠0),点 P 的运动时间为t 秒,求 S 与 t 之间的函数关系式(要求写出自变量 t 的取值范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com