
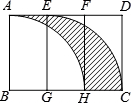
 如图,长方形ABCD的长BC为3cm,宽AB为2cm,点E、F是边AD的三等分点,点G、H是边BC的三等分点.现分别以B、G两点为圆心,以2cm长为半径画弧AH和弧EC,则阴影部分的面积为2cm2.
如图,长方形ABCD的长BC为3cm,宽AB为2cm,点E、F是边AD的三等分点,点G、H是边BC的三等分点.现分别以B、G两点为圆心,以2cm长为半径画弧AH和弧EC,则阴影部分的面积为2cm2.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明每天早上步行到学校上学.一天,小明从家里出发后5分钟时,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,并在途中追上小明,设小明离开家的时间为x(分),如图图象中的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系,请分析图中的信息并解答下列问题:
小明每天早上步行到学校上学.一天,小明从家里出发后5分钟时,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,并在途中追上小明,设小明离开家的时间为x(分),如图图象中的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系,请分析图中的信息并解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{9}$ | D. | $-2\sqrt{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com