
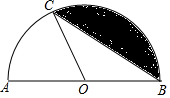
 如图,AB为半圆O的直径,C为半圆上一点,且∠COA=60°,扇形AOC的面积为$\frac{2}{3}$π,则阴影部分的面积为( )
如图,AB为半圆O的直径,C为半圆上一点,且∠COA=60°,扇形AOC的面积为$\frac{2}{3}$π,则阴影部分的面积为( )| A. | $\frac{2}{3}$π | B. | $\frac{4}{3}$π | C. | $\frac{4}{3}$π-2$\sqrt{3}$ | D. | $\frac{4}{3}$π-$\sqrt{3}$ |
分析 根据∠COA=60°,扇形AOC的面积为$\frac{2}{3}$π求得圆的半径,作CD⊥AB于点D,求出CD的长,再根据阴影部分的面积S=S扇形BOC-S△BOC计算可得.
解答 解:设圆的半径为r,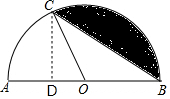
∵∠COA=60°,扇形AOC的面积为$\frac{2}{3}$π,
∴$\frac{60•π•{r}^{2}}{360}$=$\frac{2}{3}π$,
解得:r=2,
∴OB=OC=2,
过点C作CD⊥AB于点D,
∴CD=OCsin∠AOC=2×sin60°=$\sqrt{3}$,
则阴影部分的面积S=S扇形BOC-S△BOC
=$\frac{120•π•{2}^{2}}{360}$-$\frac{1}{2}$×2×$\sqrt{3}$
=$\frac{4}{3}$π-$\sqrt{3}$,
故选:D.
点评 本题主要考查扇形的面积计算,根据图形得出阴影部分的面积S=S扇形BOC-S△BOC是解题的关键.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
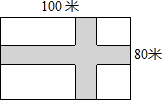 如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?
如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com