
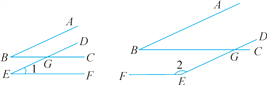
【题目】如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
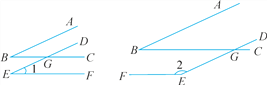
(1)∠1= ,∠2= .
(2)请观察∠1,∠2与∠ABC分别有怎样的关系,请你由此归纳一个真命题.
【答案】(1)25°,155°(2)∠1=∠ABC,∠2+∠ABC=180°
【解析】试题分析:(1)图1,已知AB∥DE,根据两直线平行,同位角相等得到∠B=∠DGC=25°,再由BC∥EF,根据两直线平行,同位角相等得∠1=∠DGC=25°;图2,已知AB∥DE,根据两直线平行,内位角相等得∠B=∠BGE=25°,再由BC∥EF,根据两直线平行,同旁内角互补得∠2+∠BGE=180°,所以∠2=155°;(2)由(1)的计算结果易得∠1与∠ABC相等,∠2与∠ABC互补,这个结论可归纳为:如果两个角的两边分别平行,那么这两个角相等或互补.
试题解析:
(1)图1,∵AB∥DE,
∴∠B=∠DGC=25°,
∵BC∥EF,
∴∠1=∠DGC=25°;
图2,∵AB∥DE,
∴∠B=∠BGE=25°,
∵BC∥EF,
∴∠2+∠BGE=180°,
∴∠2=180°-25°=155°;
故答案为25°,155°;
(2)∠1=∠ABC,∠2+∠ABC=180°.真命题:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】计算:(要求写出计算过程)
(1)5﹣(﹣6)×2÷22
(2)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣63)
)×(﹣63)
(3)(﹣2)3×( ![]() )2﹣|﹣1﹣2|
)2﹣|﹣1﹣2|
(4)![]() +
+ ![]() ﹣(﹣
﹣(﹣ ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣63);
)×(﹣63);
(2)(﹣2)2﹣5× ![]() +|﹣2|
+|﹣2|
(3)![]() +
+ ![]() ﹣|﹣2|
﹣|﹣2|
(4)﹣14﹣ ![]() ×[3﹣(﹣3)2]
×[3﹣(﹣3)2]
(5)﹣22+ ![]() ﹣6÷(﹣2)×
﹣6÷(﹣2)× ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图形1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为:1+2+3+…+n= ![]() .
.
(1)当n=15时,我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,….,则最底层最左边这个圆圈中的数是多少?当有n层时,最底层最左边这个圆圈中的数又是多少?(只列代数式不要求化简)
(2)当n=19时,我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣25,﹣24,﹣23,…则这时最底层最左边这个圆圈中的数是多少?并求出此时所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
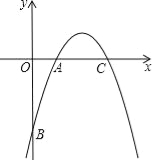
【题目】如图,已知二次函数y=﹣![]() x2+bx+c的图象经过(1,0),B(0,﹣6)两点,
x2+bx+c的图象经过(1,0),B(0,﹣6)两点,
(1)求这个二次函数解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积;
(3)根据图象,写出函数值y为负数时,自变量x的取值范围;
(4)填空:要使该二次函数的图象与x轴只有一个交点,应该把图象沿y轴向下平移 个单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 坐标为
坐标为![]() ,将正方形
,将正方形![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]()
![]() ,得到正方形
,得到正方形![]() ,
, ![]() 交线段
交线段![]() 于点
于点![]() ,
, ![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .
.

(1)求证:![]() 平分
平分 ![]() ;
;
(2)在正方形![]() 绕点
绕点![]() 逆时针旋转的过程中,求线段
逆时针旋转的过程中,求线段![]() 、
、![]() 、
、![]() 之间的数量关系;
之间的数量关系;
(3)连结![]() 、
、![]() 、
、![]() 、
、![]() ,在旋转的过程中,四边形
,在旋转的过程中,四边形![]() 是否能在点G满足一定的条件下成为矩形?若能,试求出直线
是否能在点G满足一定的条件下成为矩形?若能,试求出直线![]() 的解析式;若不能,请说明理由.
的解析式;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com