Question

12．已知：AB为⊙O直径，M、N是⊙O上的两点，且$\sqrt{2}$BM=2OB．
（1）如图1，求证：∠N=45°；
（2）如图2，若AN∥BM，C为弧AM上一点，连接CN、OC，CN与AO交于点D，若OD=CD，求证：CN=$\sqrt{3}$OB；
（3）在（2）的条件下，如图3，P为BM上的一点，若OD=$\sqrt{2}$，BP=2，求PC的长．

Answer 1

分析 （1）先判断出△BOM是等腰直角三角形，求出∠B即可得出结论；
（2）先利用三角形的外角求出∠ODN=60°，然后利用含30°角的直角三角形的性质即可得出结论；
（3）先构造出直角三角形，在Rt△CDF中，求出DF=$\frac{\sqrt{2}}{2}$，CF=$\frac{\sqrt{6}}{2}$，在Rt△PBE中，求出BE=$\sqrt{2}$，PE=$\sqrt{2}$，即可得出CG=EF=$\sqrt{6}$+$\frac{\sqrt{2}}{2}$，PG=$\sqrt{2}$-$\frac{\sqrt{6}}{2}$，最后用勾股定理求出结论即可．

解答 解：（1）连接OM，如图1，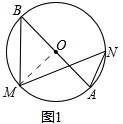
∵$\sqrt{2}$BM=2OB
∴OB=OM=$\frac{\sqrt{2}}{2}$BM，
而OB²+OM²=2OB²=2（$\frac{\sqrt{2}}{2}$BM）²=BM²，
∴△BOM为等腰直角三角形，
∴∠B=45°，
∴∠N=∠B=45°，
（2）连接ON，如图2，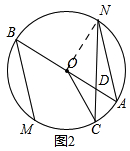
由（1）知，∠B=45°，
∵AN∥BM，
∴∠A=∠B=45°，
∴∠AON=90°，
设∠ANC=x，则∠AOC=2x，
∵OD=OC，
∴∠AOC=∠OCD
∴∠ODN=∠AOC+∠OCD=2×2x=4x，
∵∠ODN=∠A+∠ANC=45°+x，
∴4x=45°+x，
∴x=15°，
∴∠OCD=∠CAD=30°，∠ODN=60°，
在Rt△DON中，∠OND=30°，
∴OD=$\frac{\sqrt{3}}{3}$OB，DN=$\frac{2\sqrt{3}}{3}$OB，
∴CN=CD+DN=OD+DN=$\sqrt{3}$OB，
（3）如图3，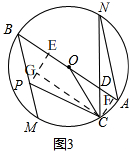
由（2）知，OD=$\frac{\sqrt{3}}{3}$OB，
∵OD=$\sqrt{2}$，
∴OB=$\sqrt{6}$，
过点P作PE⊥AB，过C作CF⊥AB，过点C作CG⊥PE，
则四边形EFCG是矩形，
∴CF=EG，CG=EF，∠CGP=90°
在Rt△CDF中，∠CDF=∠ODN=60°，CD=OD=$\sqrt{2}$，
∴DF=$\frac{\sqrt{2}}{2}$，CF=$\frac{\sqrt{6}}{2}$，
在Rt△PBE中，∠B=45°，BP=2，
∴BE=$\sqrt{2}$，PE=$\sqrt{2}$，
∴CG=EF=OB+OD+DF-BE=$\sqrt{6}$+$\sqrt{2}$+$\frac{\sqrt{2}}{2}$-$\sqrt{2}$=$\sqrt{6}$+$\frac{\sqrt{2}}{2}$，
PG=PE-CF=$\sqrt{2}$-$\frac{\sqrt{6}}{2}$，
在Rt△PGC中，PC=$\sqrt{C{G}^{2}+P{G}^{2}}$=$\sqrt{（\sqrt{6}+\frac{\sqrt{2}}{2}）^{2}+（\sqrt{2}-\frac{\sqrt{6}}{2}）^{2}}$=$\sqrt{10}$．

点评 此题是圆的综合题，主要考查了圆的性质，圆周角和圆心角的关系，勾股定理．含30°角的直角三角形的性质，矩形的判定，三角形的外角，解本题的关键是求出∠ODN，那点是构造直角三角形求出PC．