
【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M,N分别为AC,BC的中点. ![]()
(1)求线段BC,MN的长;
(2)若C在线段AB的延长线上,且满足AC﹣BC=acm,M,N分别是线段AC,BC的中点,请画出图形,并用a的式子表示MN的长度.
【答案】
(1)解:∵M是AC的中点,
∴MC= ![]() AC=3cm,
AC=3cm,
∴BC=MB﹣MC=7cm,
又N为BC的中点,
∴CN= ![]() BC=3.5cm,
BC=3.5cm,
∴MN=MC+NC=6.5cm
(2)解:如图:
![]()
∵M是AC的中点,
∴CM= ![]() AC,
AC,
∵N是BC的中点,
∴CN= ![]() BC,
BC,
∴MN=CM﹣CN= ![]() AC﹣
AC﹣ ![]() BC=
BC= ![]() (AC﹣BC)=
(AC﹣BC)= ![]() acm
acm
【解析】(1)根据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用BC=MB﹣MC,MN=CM+CN即可求出线段BC,MN的长度即可.(2)先画图,再根据线段中点的定义得MC= ![]() AC,NC=
AC,NC= ![]() BC,然后利用MN=MC﹣NC得到MN=
BC,然后利用MN=MC﹣NC得到MN= ![]() acm.
acm.
【考点精析】通过灵活运用两点间的距离,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记即可以解答此题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
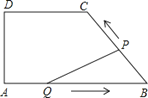
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象法求方程的解,体现了数形结合的方法,它是将方程的解看成两个函数图象交点的横坐标.若关于x的方程x2+a﹣![]() =0(a>0)只有一个整数解,则a的值等于 .
=0(a>0)只有一个整数解,则a的值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,﹣3)和点B(3,m),且AB平行于x轴,则点B坐标为( )
A. (3,﹣3) B. (3,3) C. (3,1) D. (3,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com