
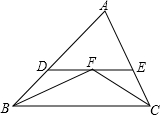
 如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
分析 由△ABC中,∠ABC与∠ACB的平分线交于点F,DE∥BC,易证得△BDF和△CEF都是等腰三角形,继而可得DE=BD+CE,又由△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;即可得△ADE的周长等于AB与AC的和.
解答 解:∵∠ABC与∠ACB的平分线交于点F,
∴∠FBC=∠ABF,∠FCB=∠ACF,
∴∠A=2∠BFC-180°,
故①正确;
∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵△ABC中,∠ABC与∠ACB的平分线交于点F,
∴∠DBF=∠FBC,∠ECF=∠FCB,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EF=EC,
∴DE=DF+EF=BD+CE,
故②正确;
∴△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;
故③正确
∵∠ABC不一定等于∠ACB,
∴∠FBC不一定等于∠FCB,
∴BF与CF不一定相等,无法判断其大小,
故④错误;
故选C
点评 此题考查了等腰三角形的性质与判定以及角平分线的定义.此题难度适中,注意掌握数形结合思想与转化思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
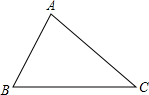 如图,利用尺规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等(保留作图痕迹,不写作法).
如图,利用尺规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
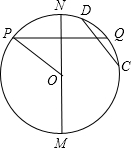 由垂径定理可知:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.请利用这一结论解决问题:
由垂径定理可知:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.请利用这一结论解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
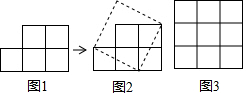
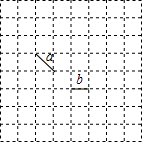 如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)
如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
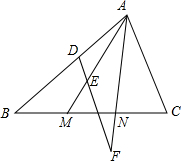 如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.
如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
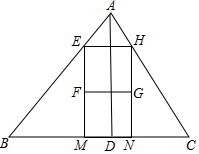 在△ABC中,已知边BC=12,该边上的高线AD=8,同样大小的两个正方形FMNG与EFGH按如图所示方式叠放,其中顶点M、N在BC边上,E、H分别在AB、AC上,求正方形的边长.
在△ABC中,已知边BC=12,该边上的高线AD=8,同样大小的两个正方形FMNG与EFGH按如图所示方式叠放,其中顶点M、N在BC边上,E、H分别在AB、AC上,求正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com