
【题目】如图1,在正方形ABCD中,P是对角线BD上的点,点E在AB上,且PA=PE.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,试探究∠CPE与∠ABC之间的数量关系,并说明理由.
【答案】
(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
 ,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)解:由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∵PA=PE,
∴∠PAE=∠PEA,
∴∠CPB=∠AEP,
∵∠AEP+∠PEB=180°,
∴∠PEB+∠PCB=180°,
∴∠ABC+∠EPC=180°,
∵∠ABC=90°,
∴∠EPC=90°
(3)∠ABC+∠EPC=180°,
理由:解:在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
 ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP,
∵PA=PE,
∴∠DAP=∠DCP,
∴∠PAE=∠PEA,
∴∠CPB=∠AEP,
∵∠AEP+∠PEB=180°,
∴∠PEB+∠PCB=180°,
∴∠ABC+∠EPC=180°
【解析】(1)根据正方形的性质,四边相等,四个角为90°,且对角线平分对角,即可证出△ABP≌△CBP(SAS),得PA=PC,由于PA=PE,得PC=PE
(2)利用全等的性质,由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PE,∠PAE=∠PEA,最后通过同角的补角的关系得到∠ABC+∠EPC=180°,以及四边形的内角和为360°,∠CPF=∠EDF=90°最后得出结论
(3)此题为一二题的变式题,借助(1)和(2)证明方法第三题易证,且菱形和正方形除了每个角不是直角以为,其他的性质都是共性,即可证出△ABP≌△CBP(SAS),得到∠BAP=∠BCP,然后根据等腰三角形的等边对等角得∠DAP=∠DCP,最后再通过同角的补角关系和四边形的内角和为360°即可得出结论。
【考点精析】关于本题考查的菱形的性质和正方形的性质,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】以下各组线段为边,能组成三角形的是( )
A. 8cm,6cm,4cm B. 2cm,4cm,6cm
C. 14cm,6cm,7cm D. 2cm,3cm,6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式4x2﹣16y2的结果是( )
A.(2x﹣4y)2
B.(2x﹣4y)(2x+4y)
C.4(x2﹣4y2)
D.4(x﹣2y)(x+2y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C( ![]() ,1),点M是射线OC上一动点.
,1),点M是射线OC上一动点.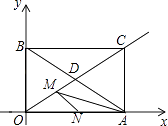
(1)求证:△ACD是等边三角形;
(2)若△OAM是等腰三角形,求点M的坐标;
(3)若N是OA上的动点,则MA+MN是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x-y=7; ②4x+1=x-y; ③![]() +y=5; ④x=y; ⑤x2-y2=2
+y=5; ④x=y; ⑤x2-y2=2
⑥6x-2y ⑦x+y+z=1 ⑧y(y-1)=2y2-y2+x
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉的爸爸买了某演唱会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果;
(2)哥哥设计的游戏规则公平吗?为什么?若不公平,请设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
 (3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com