
【题目】在Rt△ABC中,BC=AC,∠ACB=90°,点D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上,分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE、BF.
(1)当点D在线段AB上时(点D不与点A、B重合),如图1
①请你将图形补充完整;
②线段BF、AD所在直线的位置关系为 ,线段BF、AD的数量关系为 ;
(2)当点D在线段AB的延长线上时,如图2
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.

【答案】(1)①补图见解析;②垂直、相等;(2)①补图见解析;②成立,理由见解析.
【解析】试题分析:(1)①D在线段AB上时,在直线l上截取CE=CF=CD,即可画出图象.②在图1中证明△ACD≌△BCF得到AD=BF,∠BAC=∠FBC,利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
(2)①D在线段AB延长线上时,在直线l上截取CE=CF=CD,即可画出图象.②在图2中证明△ACD≌△BCF得到AD=BF,∠BAC=∠FBC,利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
试题解析:解:(1)①见图1所示.
②证明:∵CD⊥EF,∴∠DCF=90°.∵∠ACB=90°,∴∠ACB=∠DCF,∴∠ACD=∠BCF
∵BC=AC,CD=CF,∴△ACD≌△BCF,∴AD=BF,∠BAC=∠FBC,∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
故答案为:垂直、相等.
(2)①见图2所示.
②成立.理由如下:
证明:∵CD⊥EF,∴∠DCF=90°.∵∠ACB=90°,∴∠DCF+∠BCD=∠ACB+∠BCD,即∠ACD=∠BCF.∵BC=AC,CD=CF,∴△ACD≌△BCF,∴AD=BF,∠BAC=∠FBC,∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.



 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:


(1)在这次抽样调查中,一共抽取了______名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
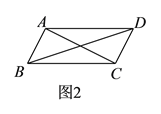
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
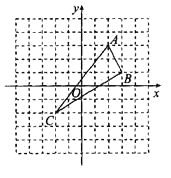
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A,B,C的对称点分别是A′,B′,C′),并直接写出A′,B′,C′的坐标.
(2)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB//DE,AC//DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )

A. AB=DE B. EF=BC C. ∠B=∠E D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( ) 
A.4米
B.2米
C.1.8米
D.3.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,平行四边形
,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .将直线
.将直线![]() 绕点
绕点![]() 顺时针旋转分别交
顺时针旋转分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.

(![]() )在旋转过程中,线段
)在旋转过程中,线段![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(![]() )如图
)如图![]() ,若
,若![]() ,当旋转角至少为__________
,当旋转角至少为__________![]() 时,四边形
时,四边形![]() 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com