
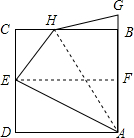
 将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$.
将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$. 分析 设正方形纸片ABCD的边长为2a,根据折叠的性质得到DE=CE=$\frac{1}{2}$CD=a,由勾股定理得到AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{5}$a,由折叠的性质得到AG=AE=$\sqrt{5}$a,HG=EH,求得BG=($\sqrt{5}$-2)a,根据勾股定理列方程得到BH=($\sqrt{5}$-1)a,即可得到结论.
解答 解:设正方形纸片ABCD的边长为2a,
∵将正方形纸片ABCD按如图所示对折,使边AD与BC重合,
∴DE=CE=$\frac{1}{2}$CD=a,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{5}$a,
∵将AE折叠到AB上,
∴AG=AE=$\sqrt{5}$a,HG=EH,
∴BG=($\sqrt{5}$-2)a,
∴CE2+CH2=BH2+BG2,
即a2+(2a-BH)2=BH2+[($\sqrt{5}$-2)a]2,
解得:BH=($\sqrt{5}$-1)a,
∴$\frac{BH}{BC}$=$\frac{(\sqrt{5}-1)a}{2a}$=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了折叠的性质,正方形的性质,勾股定理,熟练掌握折叠的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
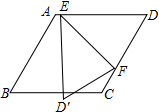 如图,在菱形ABCD中,对角线长AC=2,BD=2$\sqrt{3}$,点E、F在边AD、CD上,以直线EF为折痕折叠,若ED⊥ED′,则∠D′FC的度数为30°.
如图,在菱形ABCD中,对角线长AC=2,BD=2$\sqrt{3}$,点E、F在边AD、CD上,以直线EF为折痕折叠,若ED⊥ED′,则∠D′FC的度数为30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
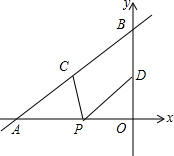 如图,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
如图,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )| A. | (-3,0) | B. | (-6,0) | C. | (-$\frac{3}{2}$,0) | D. | (-$\frac{5}{2}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
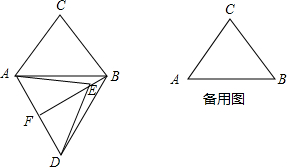
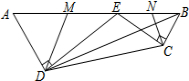 如图,在四边形ABCD中,E为AB边上一点,ED⊥AD于D,EC⊥CB于C,且∠AED=∠BEC,AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,M、N分别为AE、BE的中点,连接DM、CN,则△DEM与△CEN的周长之和为2$\sqrt{13}$+6.
如图,在四边形ABCD中,E为AB边上一点,ED⊥AD于D,EC⊥CB于C,且∠AED=∠BEC,AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,M、N分别为AE、BE的中点,连接DM、CN,则△DEM与△CEN的周长之和为2$\sqrt{13}$+6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com