
【题目】如图,甲楼AB高20m,乙楼CD高10m,两栋楼之间的水平距离BD=20m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小丽在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求电视塔的高度EF.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
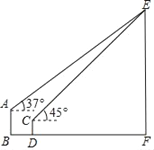
【答案】电视塔的高度EF约为110m.
【解析】
作AM⊥EF、CN⊥EF,设EN=xm,由∠ECN=45°知CN=EN=xm,根据BD=20m、AB=MF=10m、CD=NF=10m可得AM=x+20、EM=x﹣10,由tan∠EAM=![]() 列出关于x的方程,解之求得x的值即可得.
列出关于x的方程,解之求得x的值即可得.
如图所示,过点A作AM⊥EF于点M,过点C作CN⊥EF于点N,
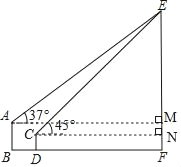
设EN=xm,
∵∠ECN=45°,
∴CN=EN=xm,
∵BD=20m,AB=MF=10m,CD=NF=10m,
∴AM=BF=BD+DF=BD+CN=x+20(m),EM=EN﹣MN=EN﹣(MF﹣NF)=x﹣10(m),
∵tan∠EAM=![]() ,
,
∴![]() =0.75,
=0.75,
解得:x=100,
则EF=110m,
答:电视塔的高度EF约为110m.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
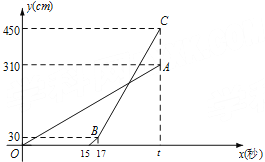
【题目】甲乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.两机器人行走的路程y(cm)与时间x(s)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)乙比甲晚出发_________秒,乙提速前的速度是每秒_________cm, ![]() =_________;
=_________;
(2)已知甲匀速走完了全程,请补全甲的图象;
(3)当x为何值时,乙追上了甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点作圆,点
三点作圆,点![]() 在第一象限部分的圆上运动,连结
在第一象限部分的圆上运动,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() 的最大值为10.其中正确的是( )
的最大值为10.其中正确的是( )
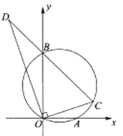
A. ①②B. ②③C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,点
,点![]() 是抛物线上第二象限内一点.
是抛物线上第二象限内一点.
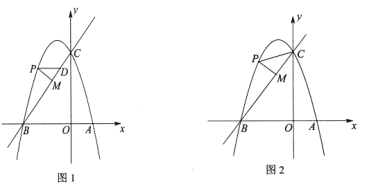
(1)求二次函数和一次函数的表达式;
(2)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,作
,作![]() 的垂线
的垂线![]() 交
交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的周长为
的周长为![]() .
.
①求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
②求![]() 的周长的最大值及此时点
的周长的最大值及此时点![]() 的坐标;
的坐标;
(3)如图2,连接![]() ,是否存在点
,是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,直接写出点
相似?若存在,直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图反映了我国最近十年间核电发电量的增长情况,根据统计图提供的信息,下列判断合理的是( )
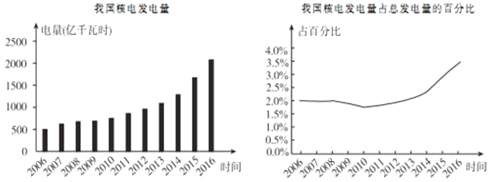
A. 2011年我国的核电发电量占总发电量的比值约为1.5%
B. 2006年我国的总发电量约为25000亿千瓦时
C. 2013年我国的核电发电量占总发电量的比值是2006年的2倍
D. 我国的核电发电量从2008年开始突破1000亿千瓦时
查看答案和解析>>
科目:初中数学 来源: 题型:
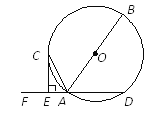
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
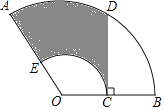
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com