
����Ŀ���Ķ�������ϣ�
��ͼ1����ƽ��ֱ������ϵxOy�У�ֱ��y1=ax+b��˫����y2= ![]() ����A��1��3����B����3����1�����㣮
����A��1��3����B����3����1�����㣮
�۲�ͼ���֪��
�ٵ�x=��3��1ʱ��y1=y2��
�ڵ���3��x��0��x��1ʱ��y1��y2 �� ��ͨ���۲캯����ͼ���Եõ�����ʽax+b�� ![]() �Ľ⼯��
�Ľ⼯��
������һ�����⣺��ʽx3+4x2��x��4��0�Ľ⼯��
ijͬѧ����ѧϰ����֪ʶ�ľ��飬����ʽx3+4x2��x��4��0�Ľ⼯������̽����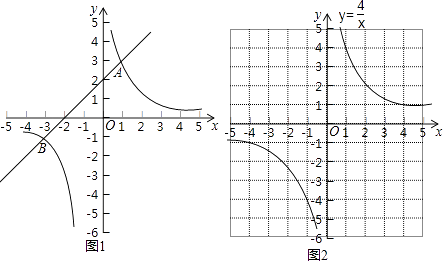
����������̽�����̣��뽫��2������3������4������������
��1��������ʽ����������ת����
��2�����캯��������ͼ��
��y3=x2+4x��1��y4= ![]() ����ͬһ����ϵ�зֱ�������������ͼ��
����ͬһ����ϵ�зֱ�������������ͼ��
˫����y4= ![]() ��ͼ2��ʾ�����ڴ�����ϵ�л���������y3=x2+4x��1���������б���
��ͼ2��ʾ�����ڴ�����ϵ�л���������y3=x2+4x��1���������б���
��3��ȷ����������ͼ����ĺ����꣬�۲���������������ͼ���벢ͨ�����뺯������ʽ��֤��֪������y3=y4������x��ֵΪ
��4������ͼ��д���⼯
��ϣ�1�������۽�����۲�����������ͼ���֪������ʽx3+4x2��x��4��0�Ľ⼯
���𰸡�
��1���⣺��x=0ʱ��ԭ����ʽ��������
��x��0ʱ��ԭ����ʽ����ת��Ϊx2+4x��1�� ![]() ��
��
��x��0ʱ��ԭ����ʽ����ת��Ϊx2+4x��1�� ![]() ��
��
��2���⣺
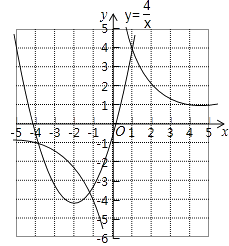
��3����1�ͩ�4
��4��x��1��4��x����1
���������⣺��2��  ����3����������ͼ����ĺ������ǡ�1�ͩ�4��
����3����������ͼ����ĺ������ǡ�1�ͩ�4��
������y3=y4������x��ֵΪ��1�ͩ�4��
�ʴ��ǣ���1�ͩ�4����4������ʽx3+4x2��x��4��0����x��0ʱ��x2+4x��1�� ![]() ����ʱx�ķ�Χ�ǣ�x��1��
����ʱx�ķ�Χ�ǣ�x��1��
��x��0ʱ��x2+4x��1�� ![]() ����4��x����1��
����4��x����1��
�ʴ��ǣ�x��1��4��x����1��
��2������ȷ�����κ����ĶԳ��ᣬȻ��ȷ�������㼴���������κ�����ͼ��3������ͼ��ֱ����⣻��4��������֪����ʽx3+4x2��x��4��0����x��0ʱ��x2+4x��1�� ![]() ������x��0ʱ��x2+4x��1��
������x��0ʱ��x2+4x��1�� ![]() ������ͼ��ֱ��д���𰸣�
������ͼ��ֱ��д���𰸣�


 ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д� ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��ѧϰ��Բ����һ��ʱ����ʦ��ͬѧ�Dz�����һ���߹���ͼ�⣺
�߹���ͼ����Բ��һ����Բ�����ߡ�
��֪��PΪ��O��һ�㡣
������������P�ġ�O������
С�����������£�
��ͼ��
������OP�����߶�OP�Ĵ�ֱƽ����MN��OP��C
���Ե�CΪԲ�ģ�CO�ij�Ϊ�뾶��Բ������O ��A��B����
����ֱ��PA��PB����ֱ��PA��PB�������������
��ʦ��ΪС����������ȷ��
��ش�����OA��OB��֤��OAP=��OBP=90�㣬�����������ɴ˿�֤��ֱ��PA��PB���ǡ�O�����ߣ��������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨��ƽ���ڵ�A��ͼ��G�ϸ�����ľ������Сֵ��Ϊ�õ㵽���ͼ�ε���С����d����A��ͼ��G�ϸ�����ľ�������ֵ��Ϊ�õ㵽���ͼ�ε�������D�������A��ͼ��G�ľ�����ΪR=D��d��
��1������ͼ1����ƽ��ֱ������ϵxOy�У�ͼ��G1Ϊ��OΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��д�����¸��㵽ͼ��G1�ľ����ȣ�
A����1��0���ľ�������
B�� ![]() ����
���� ![]() ���ľ�������
���ľ�������
C����3��2���ľ�������
�ڸ��ݢ��еĽ�������뵽ͼ��G1�ľ�����Ϊ2�����еĵ���ɵ�ͼ�ε���״�� �� 
��2����ͼ2����ƽ��ֱ������ϵxOy�У�ͼ��G2Ϊ��C��1��0��ΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��y=k��x+1���ϴ��ڵ�G2�ľ�����Ϊ2�ĵ㣬��k��ȡֵ��Χ�� 
��3����ͼ3����ƽ��ֱ������ϵxOy�У�����OA��y= ![]() x��x��0����ԲC����3Ϊ�뾶��Բ����Բ��C��x�����˶���������OA�ϴ��ڵ㵽ԲC�ľ�����Ϊ2��ֱ��д��Բ��C�ĺ�����xc��ȡֵ��Χ��
x��x��0����ԲC����3Ϊ�뾶��Բ����Բ��C��x�����˶���������OA�ϴ��ڵ㵽ԲC�ľ�����Ϊ2��ֱ��д��Բ��C�ĺ�����xc��ȡֵ��Χ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУҪΧһ�����λ��ԣ���һ�������㹻����ǽ�������������Χ�ɣ���������Ҫ����Ҫ��һ����ʽ����Էָ�Ϊ����С���β��֣���ͼ��ʾ�����ܹ�36�����ǡ�����꣨��������ģ�������δ�ֱ��ǽ���һ��AB�ij�Ϊx�ף�Ҫ��AB��AD�������λ���ABCD�����ΪSƽ���ף� 
��1����S��x֮��ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��2��Ҫ��ʹ���λ���ABCD��������AB�ߵij�ӦΪ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�����һ���ṹ��ͬ��ѧ�������������Щ����ذ���Ҫ�̴�ש��һ��4��һ������ȥ��4�����ᣬ�����ʣ12 m2����δ�̴�ש��ͬ��ʱ����6������������4������պ���ɣ���֪ÿ��һ�������ȶ�������һ�����3 m2��ש��
(1)��ÿ��������Ҫ�̴�ש�ĵذ������
(2)�ָ�ѧУ��20������ĵذ��36 m2��������Ҫ�̴�ש��ij���̶���4��һ��������6������������һ��ʼ��4��һ���������̴�ש��3���ѧУ����ʵ�����Ҫ��2���������ʣ����������Ծ�������һ����������һ����������Ҫ�ٰ��Ŷ����������������ܰ�ʱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���BD�Ĵ�ֱƽ����MN��AD�ཻ�ڵ�M����BD�ཻ�ڵ�N������BM��DN��

��1����֤���ı���BMDN�����Σ�
��2����AB=4��AD=8����MD�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ���㣨1��0���ں���ͼ���ϣ���ôabc��2a+b��a+b+c��a��b+c���ĸ�����ʽ�У�ֵ���ڻ����������У� �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����B=��DEF��AB=DE��Ҫ˵����ABC�ա�DEF.��1��������ASA��Ϊ���ݣ���ȱ���� _________________ ����2��������AAS��Ϊ���ݣ���ȱ����___________________����3��������SAS��Ϊ���ݣ���ȱ����___________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��������·ݳ���ͬһƷ�Ƹ��ֹ��յ�����̨�����±����ش�
|
|
|
| |
���� |
|
|
|
|
���� |
|
|
|
|
![]() �̵�ƽ��ÿ�����ۿյ�________̨��
�̵�ƽ��ÿ�����ۿյ�________̨��
![]() �̵���۸��ֹ��Ŀյ��У�������________ƥ��
�̵���۸��ֹ��Ŀյ��У�������________ƥ��
![]() ���о����·ݽ���ʱ���̵꾭������________��ƥ���Ŀյ�Ҫ�����________��ƥ���Ŀյ�Ҫ�ٽ���
���о����·ݽ���ʱ���̵꾭������________��ƥ���Ŀյ�Ҫ�����________��ƥ���Ŀյ�Ҫ�ٽ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com