
【题目】如图1,抛物线y=ax2-4ax+b交x轴正半轴于A,B两点,交y轴正半轴于C,且OB=OC=3.
(1)求抛物线的解析式;
(2)点D为抛物线的顶点,点G在直线BC上,若![]() ,直接写出点G的坐标;
,直接写出点G的坐标;
(3)将抛物线向上平移m个单位,交BC于点M,N(如图2),若∠MON=45°,求m的值.

【答案】(1)y=x2-4x+3;(2)![]() ;(3)m=
;(3)m=![]()
【解析】试题分析: ![]() 把
把![]() 代入
代入![]() 解方程组即可.
解方程组即可.![]() 直线BC:y=-x+3,设点
直线BC:y=-x+3,设点![]() 根据两点之间的距离公式,列出式子,求出
根据两点之间的距离公式,列出式子,求出![]() 的值.
的值.
(3)如图2中,将△OCM绕点O顺时针旋转90°得到△OBG.首先证明MN2=CM2+BN2,设![]() 则
则![]() 设平移后的抛物线的解析式为
设平移后的抛物线的解析式为![]() 由
由![]() 消去
消去![]() 得到
得到![]() 由
由
 ,推出
,推出![]()
![]() 关于直线
关于直线![]() 对称,所以
对称,所以![]() 设
设![]() 则
则![]() 利用勾股定理求出
利用勾股定理求出![]() 以及
以及![]() 的长,再根据根与系数关系,列出方程即可解决问题.
的长,再根据根与系数关系,列出方程即可解决问题.
试题解析:(1)∵OB=OC=3,
![]() 代入
代入![]()
得![]() 解得
解得![]()
∴抛物线的解析式为y=x2-4x+3.
(2)直线BC: ![]() 设点
设点![]()
顶点![]() 的坐标为:
的坐标为: ![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
(3)如图2中,将△OCM绕点O顺时针旋转90°得到△OBG.

∵∠MON=45°,
∴∠MOC+∠NOB=∠NOB+∠BOG=45°,
∴∠MON=∠GON=45°,∵ON=ON,OM=OG,
∴△ONM≌△ONG,
∴MN=NG,
∵∠NBG=∠NBO+∠OBG=45°+45°=90°,
∴NG2=BN2+BG2,
∴MN2=CM2+BN2,
设平移后的抛物线的解析式为y=x2-4x+3+m, M(x1,y1),N(x2,y2),
则![]()
设平移后的抛物线的解析式为![]()
由![]() 消去
消去![]() 得到
得到![]()
 ,推出
,推出![]()
![]() 关于直线
关于直线![]() 对称,所以
对称,所以![]() 设
设![]() 则
则![]() ∴
∴
![]()
![]() (负根已经舍弃),
(负根已经舍弃),
![]()
![]()
![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数 y=![]() 的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,回答当一次函数的值大于反比例函数的值时,x 的取值范围为________;
(3) 连接AO、BO,则△ABO的面积是_________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A的坐标;
(2)当S△ABC=15时,求该抛物线的表达式;
(3)在(2)的条件下,经过点C的直线![]() 与抛物线的另一个交点为D.该抛物线在直线
与抛物线的另一个交点为D.该抛物线在直线![]() 上方的部分与线段CD组成一个新函数的图象。请结合图象回答:若新函数的最小值大于﹣8,求k的取值范围.
上方的部分与线段CD组成一个新函数的图象。请结合图象回答:若新函数的最小值大于﹣8,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
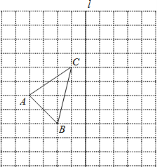
【题目】(2013年四川眉山8分)如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
(2)作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C;
(3)在(2)的条件下直接写出点B旋转到B2所经过的路径的长.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
(1)求b+c的值;
(2)若点C在抛物线上,且四边形OABC是平行四边形,求抛物线的解析式;
(3)在(2)条件下,点P(不与A,C重合)是抛物线上的一点,点M是y轴上一点,当△BPM是等腰直角三角形时,直接写出点M的坐标..

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1,(只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2,(只画出图形),写出B2和C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达点B为止;点Q以2 cm/s的速度向点D移动。经过长时间P、Q两点之间的距离是10 cm?(8′)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com