
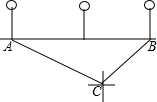
 周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:
周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:分析 过点C作CD⊥AB于点D,设CDx米,在Rt△ACD和Rt△BCD中,根据三角函数分别求出AD和BD,再根据AB=AD+BD,求出x的值即可得出答案.
解答 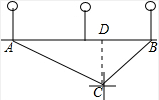 解:如图,过点C作CD⊥AB于点D,设CDx米,
解:如图,过点C作CD⊥AB于点D,设CDx米,
在Rt△ACD中,
∵∠ACD=64°,
∴AD=CD•tan64°=tan64°x(米),
在Rt△BCD中,
∴∠DCB=44°,
∴BD=CD•tan44°=tan44°x(米),
∵AB=AD+BD,
∴AB=tan64°x+tan44°x=50×2=100,
解得:x≈32,
答:此时小明一家离岸边的距离约32米.
点评 此题考查了解直角三角形的应用,此类问题比较简单,在解答过程中,正确使用三角函数是解题的关键.


科目:初中数学 来源: 题型:解答题
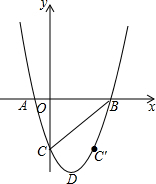 已知:抛物线y=x2-4x-m(m>0)与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,C点关于抛物线对称轴的对称点为C′点.
已知:抛物线y=x2-4x-m(m>0)与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,C点关于抛物线对称轴的对称点为C′点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com