
 如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.分析 (1)由已知角相等,及对顶角相等得到三角形DOE与三角形POB相似,利用相似三角形对应角相等得到∠OBP为直角,即可得证;
(2)在直角三角形PBD中,由PB与DB的长,利用勾股定理求出PD的长,由切线长定理得到PC=PB,由PD-PC求出CD的长,在直角三角形OCD中,设OC=r,则有OD=12-r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,即为圆的半径
解答 解:
(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线;
(2)在Rt△PBD中,PB=9,DB=12,
根据勾股定理得:PD=$\sqrt{P{B}^{2}+D{B}^{2}}$=15,
∵PD与PB都为圆的切线,
∴PC=PB=9,
∴DC=PD-PC=15-9=6,
在Rt△CDO中,设OC=r,则有DO=12-r,
根据勾股定理得:(12-r)2=r2+62,
解得:r=4.5,
则圆的半径为4.5.
点评 此题考查了切线的判定与性质,勾股定理,熟练掌握切线的判定与性质是解本题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
| 每天售出的冰箱台数(台) | 每台冰箱的利润(元) | |
| 降价前 | 8 | 400 |
| 降价后 | 8+$\frac{x}{50}$×4 | 400-x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
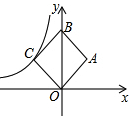 如图,在平面直角坐标系中,正方形OABC的面积为24,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k=-12.
如图,在平面直角坐标系中,正方形OABC的面积为24,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k=-12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
| 出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
| 温州南 | 雁落山 | 26 | 22 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031.
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com