
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨ AB=AC=10£¨œþ∂ŒBC‘⁄![]() ÷·…œ£¨BC=12£¨µ„Bµƒ◊¯±ÍŒ™£®£≠3£¨0£©£¨œþ∂ŒABΩª
÷·…œ£¨BC=12£¨µ„Bµƒ◊¯±ÍŒ™£®£≠3£¨0£©£¨œþ∂ŒABΩª![]() ÷·”⁄µ„E£¨π˝A◊˜AD°ÕBC”⁄D£¨∂ص„P¥”‘≠µ„≥ˆ∑¢£¨“‘√ø√Î3∏ˆµ•ŒªµƒÀŸ∂»—ÿ
÷·”⁄µ„E£¨π˝A◊˜AD°ÕBC”⁄D£¨∂ص„P¥”‘≠µ„≥ˆ∑¢£¨“‘√ø√Î3∏ˆµ•ŒªµƒÀŸ∂»—ÿ![]() ÷·œÚ”“‘À∂Ø£¨…Ë‘À∂صƒ ±º‰Œ™
÷·œÚ”“‘À∂Ø£¨…Ë‘À∂صƒ ±º‰Œ™![]() √ΣÆ
√ΣÆ
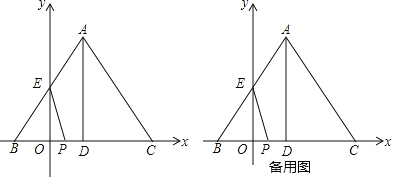
£®1£©µ±°˜BPE «µ»—¸»˝Ω«–Œ ±£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©»Ùµ„P‘À∂صƒÕ¨ ±£¨°˜ABC“‘BŒ™ŒªÀ∆÷––ƒœÚ”“∑≈¥Û£¨«“µ„CœÚ”“‘À∂صƒÀŸ∂»Œ™√ø√Î2∏ˆµ•Œª£¨°˜ABC∑≈¥ÛµƒÕ¨ ±∏þAD“≤ÀÊ÷Æ∑≈¥Û£¨µ±“‘EPŒ™÷±æ∂µƒ‘≤”Î∂Øœþ∂ŒADÀ˘‘⁄÷±œþœý«– ±£¨«Û![]() µƒ÷µ∫Õ¥À ±µ„Cµƒ◊¯±Í£Æ
µƒ÷µ∫Õ¥À ±µ„Cµƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©t=![]() ªÚt=1ªÚt=
ªÚt=1ªÚt=![]() £ª£®2£©µ±t=1 ±°—F”Î∂Øœþ∂ŒADÀ˘‘⁄÷±œþœý«–£¨¥À ±C£®11£¨0£©£Æ
£ª£®2£©µ±t=1 ±°—F”Î∂Øœþ∂ŒADÀ˘‘⁄÷±œþœý«–£¨¥À ±C£®11£¨0£©£Æ
°æΩ‚Œˆ°ø
£®1£© ◊œ»«Û≥ˆ÷±œþABµƒΩ‚Œˆ Ω£¨Ω¯∂¯∑÷±¿˚”√¢Ÿµ±BE£ΩBP ±£¨¢⁄µ±EB£ΩEP ±£¨¢€µ±PB£ΩPE ±£¨µ√≥ˆtµƒ÷µº¥ø…£ª
£®2£© ◊œ»µ√≥ˆ°˜PGF°◊°˜POE£¨‘Ÿ¿˚”√‘⁄Rt°˜EOP÷–£∫EP2£ΩOP2£´EO2£¨Ω¯∂¯«Û≥ˆtµƒ÷µ“‘º∞Cµ„◊¯±Í£Æ
£®1£©°þAB=AC£¨AD°ÕBC£¨
°ýBD=CD=6£¨
°þAB=10£¨°ýAD=8£¨°ýA£®3£¨8£©£¨
…Ë÷±œþABµƒΩ‚Œˆ ΩŒ™£∫y=kx+b£¨‘Ú![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨
°ý÷±œþABµƒΩ‚Œˆ ΩŒ™£∫y=![]() x+4£¨
x+4£¨
°ýE£®0£¨4£©£¨
°ýBE=5£¨
µ±°˜BPE «µ»—¸»˝Ω«–Œ”–»˝÷÷«Èøˆ£∫
¢Ÿµ±BE=BP ±£¨3+3t=5£¨Ω‚µ√£∫t=![]() £ª
£ª
¢⁄µ±EB=EP ±£¨3t=3£¨Ω‚µ√£∫t=1£ª
¢€µ±PB=PE ±£¨
°þPB=PE£¨AB=AC£¨°œABC=°œPBE£¨
°ý°œPEB=°œACB=°œABC£¨
°ý°˜PBE°◊°˜ABC£¨
°ý![]() £¨
£¨
°ý![]() £¨Ω‚µ√£∫t=
£¨Ω‚µ√£∫t=![]() £¨
£¨
◊€…œ£∫t=![]() ªÚt=1ªÚt=
ªÚt=1ªÚt=![]() £ª
£ª
£®2£©”…“‚µ√£∫C£®9+2t£¨0£©£¨
°ýBC=12+2t£¨BD=CD=6+t£¨OD=3+t£¨
…ËFŒ™EPµƒ÷–µ„£¨¡¨Ω”OF£¨◊˜FH°ÕAD£¨FG°ÕOP£¨
°þFG°ŒEO£¨
°ý°˜PGF°◊°˜POE£¨
°ýPG=OG=![]() t£¨FG=
t£¨FG=![]() EO=2£¨°ýF£®
EO=2£¨°ýF£®![]() t£¨2£©£¨
t£¨2£©£¨
°ýFH=GD=OD©ÅOG=3+t©Å![]() t=3©Å
t=3©Å![]() t£¨
t£¨
°þ°—F”Î∂Øœþ∂ŒADÀ˘‘⁄÷±œþœý«–£¨FH=![]() EP=3©Å
EP=3©Å![]() t£¨
t£¨
‘⁄Rt°˜EOP÷–£∫EP2=OP2+EO2
°ý4£®3©Å![]() t£©2=£®3t£©2+16
t£©2=£®3t£©2+16
Ω‚µ√£∫t1=1£¨t2=©Å![]() £®…·»•£©£¨
£®…·»•£©£¨
°ýµ±t=1 ±°—F”Î∂Øœþ∂ŒADÀ˘‘⁄÷±œþœý«–£¨¥À ±C£®11£¨0£©£Æ



 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
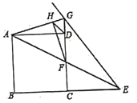
°æƒø°ø»ÁÕº£¨µ„![]() «’˝∑Ω–Œ
«’˝∑Ω–Œ![]() µƒ±þ
µƒ±þ![]() —”≥§œþ“ªµ„£¨¡¨Ω”
—”≥§œþ“ªµ„£¨¡¨Ω”![]() Ωª
Ωª![]() ”⁄
”⁄![]() £¨◊˜
£¨◊˜![]() £¨
£¨![]() Ωª
Ωª![]() µƒ—”≥§œþ”⁄
µƒ—”≥§œþ”⁄![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨µ±
£¨µ±![]()
![]() ±£¨◊˜
±£¨◊˜![]() ”⁄
”⁄![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨‘Ú
£¨‘Ú![]() µƒ≥§Œ™£® £©
µƒ≥§Œ™£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™°œACD£Ω90°„£¨AC£ΩDC£¨MN «π˝µ„Aµƒ÷±œþ£¨DB°ÕMN”⁄µ„B£Æ
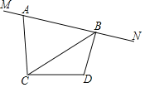
£®1£©»ÁÕº£¨«Û÷§£∫BD+AB£Ω![]() BC£ª
BC£ª
£®2£©÷±œþMN»∆µ„A–˝◊™£¨‘⁄–˝◊™π˝≥Ã÷–£¨µ±°œBCD£Ω30°„£¨BD£Ω![]() ±£¨«ÛBCµƒ÷µ£Æ
±£¨«ÛBCµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø “ªÀ“π€π‚”Œ¥¨¥”∏€ø⁄A“‘±±∆´∂´60°„µƒ∑ΩœÚ≥ˆ∏€π€π‚£¨∫Ω––80∫£¿Ô÷¡C¥¶ ±∑¢…˙¡À≤ý∑≠≥¡¥¨ ¬π £¨¡¢º¥∑¢≥ˆ¡À«Ûæ»–≈∫≈£¨“ªÀ“‘⁄∏€ø⁄’˝∂´∑ΩœÚµƒ∫£æØ¥¨Ω”µΩ«Ûæ»–≈∫≈£¨≤‚µ√ ¬π ¥¨‘⁄À¸µƒ±±∆´∂´37°„∑ΩœÚ£¨¬Ì…œ“‘40∫£¿Ô√ø–° ±µƒÀŸ∂»«∞Õ˘æ»‘Æ£¨«Û∫£æØ¥¨µΩ¥Û ¬π ¥¨C¥¶À˘–˵ƒ¥Û‘º ±º‰£Æ£®Œ¬Ð∞÷ æ£∫sin53°„°÷0.8£¨cos53°„°÷0.6£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥—ß–£Œ™‘ˆº”Ô˝πðπ€÷⁄◊¯œØ ˝¡ø£¨æˆ∂®∂‘Ô˝πðΩ¯–– ©π§∏ƒ‘ϣƻÁÕº£¨Œ™Ã”˝πð∏ƒ‘ϵƒΩÿ√Ê æ“‚Õº£Æ“—÷™‘≠◊˘Œª«¯◊Ó∏þµ„AµΩµÿ√ʵƒ«¶÷±∏þ∂»AC≥§∂»Œ™15√◊£¨‘≠∆¬√ÊABµƒ«„–±Ω«°œABCŒ™45°„£¨‘≠∆¬Ω≈B”Î≥°πð÷–—僑À∂Ø«¯±þΩÁµƒ∞≤»´æý¿ÎBDŒ™5√◊£Æ»Áπ˚∞¥’’ ©π§∑ΩÃ·π©µƒ…˺∆∑Ω∞∏ ©π§£¨–¬◊˘Œª«¯◊Ó∏þµ„EµΩµÿ√ʵƒ«¶÷±∏þ∂»EG≥§∂»±£≥÷15√◊≤ª±‰£¨ πA°¢E¡Ωµ„º‰æý¿ÎŒ™2√◊£¨ π∏ƒ‘Ï∫Û∆¬√ÊEFµƒ«„–±Ω«°œEFGŒ™37°„£Æ»Ù—ß–£“™«Û–¬∆¬Ω≈F–Ë”Î≥°πð÷–—僑À∂Ø«¯±þΩÁµƒ∞≤»´æý¿ÎFD÷¡…Ÿ±£≥÷2.5√◊£®º¥FD°ð2.5£©£¨«ÎŒ ©π§∑ΩÃ·π©µƒ…˺∆∑Ω∞∏ «∑Ò¬˙◊„∞≤»´“™«Ûƒÿ£ø«ÎÀµ√˜¿Ì”…£Æ£®≤Œøº ˝æð£∫sin37°„°÷![]() £¨tan37°„°÷
£¨tan37°„°÷![]() £©
£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™°˜ABC÷–£¨AB£ΩCB£¨D «±þACµƒ÷–µ„£¨π˝µ„D◊ˆDE°ÕBC”⁄E£Æ
£®1£©“‘±þABŒ™÷±æ∂◊˜°—O£¨◊˜Õº“™«Û£∫≥þπÊ◊˜Õº£¨±£¡Ù◊˜Õº∫€º££¨≤ª–¥◊˜∑®£ª
£®2£©‘⁄£®1£©Ãıº˛œ¬£¨≈–∂œDE”Α≤O «∑Òœý«–£ø≤¢Àµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
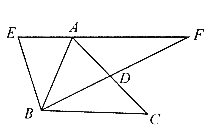
°æƒø°ø»ÁÕº£¨“—÷™![]() ÷–£¨
÷–£¨![]() £¨D «œþ∂ŒAC…œ“ªµ„£®≤ª”ÎA,C÷ÿ∫œ£©,¡¨Ω”BD£¨Ω´
£¨D «œþ∂ŒAC…œ“ªµ„£®≤ª”ÎA,C÷ÿ∫œ£©,¡¨Ω”BD£¨Ω´![]() —ÿAB∑≠’€£¨ πµ„D¬‰‘⁄µ„E¥¶£¨—”≥§BD”ÎEAµƒ—”≥§œþΩª”⁄µ„F£¨»Ù
—ÿAB∑≠’€£¨ πµ„D¬‰‘⁄µ„E¥¶£¨—”≥§BD”ÎEAµƒ—”≥§œþΩª”⁄µ„F£¨»Ù![]() «÷±Ω«»˝Ω«–Œ£¨‘ÚAFµƒ≥§Œ™_________.
«÷±Ω«»˝Ω«–Œ£¨‘ÚAFµƒ≥§Œ™_________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨µ„D‘⁄°˜ABCµƒƒ⁄≤ø«“DB=DC£¨µ„E£¨F‘⁄‘⁄°˜ABCµƒÕ‚≤ø£¨FB=FA£¨EA=EC£¨°œFBA=°œDBC=°œECA.
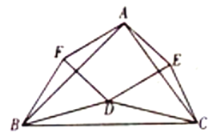
Ω‚¥œ¬¡–Œ £∫
£®1£©¢ŸÃÓø’£∫°˜ACE°◊_________°◊___________£ª
¢⁄«Û÷§£∫°˜CDE°◊°˜CBA£ª
£®2£©«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©»Ùµ„D‘⁄°œBACµƒ∆Ω∑÷œþ…œ£¨≈–∂œÀƒ±þ–ŒAFDEµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Rt°˜ABC÷–£¨°œC£Ω90°„£¨AC£Ω4£¨BC£Ω3£¨µ„D «AB±þ…œ“ªµ„£®≤ª”ÎA°¢B÷ÿ∫œ£©£¨»Ùπ˝µ„Dµƒ÷±œþΩÿµ√µƒ»˝Ω«–Œ”ΰ˜ABCœýÀ∆£¨≤¢«“∆Ω∑÷°˜ABCµƒ÷Ð≥§£¨‘ÚADµƒ≥§Œ™____£Æ
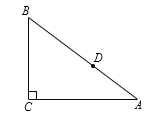
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com