
 操作园地:如图,一副直角三角板△ABC和△DEF,已知BC=DF,∠F=30°,EF=2ED,课堂上,老师将△ABC和△DEF叠加放置像图2的位置,并要求△ABC始终固定不动,将三角板△EDf绕点D逆时针旋转,探究发现图形旋转角与边之间的位置关系.
操作园地:如图,一副直角三角板△ABC和△DEF,已知BC=DF,∠F=30°,EF=2ED,课堂上,老师将△ABC和△DEF叠加放置像图2的位置,并要求△ABC始终固定不动,将三角板△EDf绕点D逆时针旋转,探究发现图形旋转角与边之间的位置关系. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 在大同市开张的美化城市活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠前,另三边用总长为40m的栅栏围成(如图所示),若设花园的BC长为x(m),花园的面积为y(m2).
在大同市开张的美化城市活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠前,另三边用总长为40m的栅栏围成(如图所示),若设花园的BC长为x(m),花园的面积为y(m2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
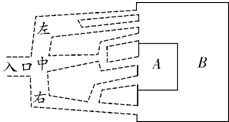 如图是“密室逃脱俱乐部”的通路俯视图,一同学进入入口后,可任选一条通道过关.
如图是“密室逃脱俱乐部”的通路俯视图,一同学进入入口后,可任选一条通道过关.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
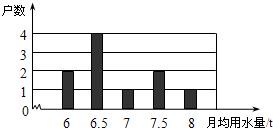 我国是世界上严重缺失的国家之一,为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如图的条形统计图,则这10个样本数据的中位数是6.5t.
我国是世界上严重缺失的国家之一,为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如图的条形统计图,则这10个样本数据的中位数是6.5t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{7}{4}$ | B. | $\frac{1}{2}$ | C. | -4 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com