
 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=74°,∠DOF=90°.
如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=74°,∠DOF=90°.分析 (1)由邻补角定义即可得出结果;
(2)由对顶角相等得出∠BOD=∠AOC=74°,由角平分线定义即可得出结果;
(3)求出∠BOF=∠DOF-∠BOD=16°,即可得出∠EOF的度数.
解答 解:(1)∵∠AOC=74°,
∴∠BOC=180°-74°=106°;
(2)∵∠BOD=∠AOC=74°,OE平分∠BOD,
∴∠BOE=$\frac{1}{2}$∠BOD=37°;
(3)∵∠BOF=∠DOF-∠BOD=90°-74°=16°,
∴∠EOF=∠BOE+∠BOF=37°+16°=53°.
点评 本题考查了邻补角定义、对顶角相等的性质以及角平分线定义;熟练掌握各个角之间的数量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
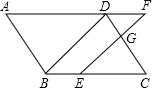 如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE=4,连接EF交CD于G.若$\frac{DG}{GC}$=$\frac{2}{3}$,求AD的长.
如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE=4,连接EF交CD于G.若$\frac{DG}{GC}$=$\frac{2}{3}$,求AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某家禽养殖场,用总长为80m的围栏靠墙(墙长为20m)围成如图所示的三块面积相等的矩形区域,设AD长为xm,矩形区域ABCD的面积为ym2.
某家禽养殖场,用总长为80m的围栏靠墙(墙长为20m)围成如图所示的三块面积相等的矩形区域,设AD长为xm,矩形区域ABCD的面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,点D在BC边上,有下列三个关系式:
如图,△ABC中,点D在BC边上,有下列三个关系式:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com