
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE. 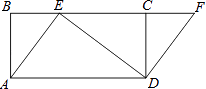
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠DCF=90°,
∵∠BAE=∠CDF,
在△ABE和△DCF中,
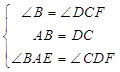 ,
,
∴△ABE≌△DCF(ASA),
∴BE=CF,
∴BC=EF,
∵BC=AD,
∴EF=AD,
又∵EF∥AD,
∴四边形AEFD是平行四边形;
(2)解:由(1)知:EF=AD=5,
在△EFD中,∵DF=3,DE=4,EF=5,
∴DE2+DF2=EF2,
∴∠EDF=90°,
∴ ![]() EDDF=
EDDF= ![]() EFCD,
EFCD,
∴CD= ![]() .
.
【解析】(1)直接利用矩形的性质结合全等三角形的判定与性质得出BE=CF,进而得出答案;(2)利用勾股定理的逆定理得出∠EDF=90°,进而得出 ![]() EDDF=
EDDF= ![]() EFCD,求出答案即可.
EFCD,求出答案即可.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图,地面上小山的两侧有![]() ,
,![]() 两地,为了测量
两地,为了测量![]() ,
,![]() 两地的距离,让一热气球从小山西侧
两地的距离,让一热气球从小山西侧![]() 地出发沿与
地出发沿与![]() 成
成![]() 角的方向,以每分钟
角的方向,以每分钟![]() 的速度直线飞行,
的速度直线飞行,![]() 分钟后到达
分钟后到达![]() 处,此时热气球上的人测得
处,此时热气球上的人测得![]() 与
与![]() 成
成![]() 角,请你用测得的数据求
角,请你用测得的数据求![]() ,
,![]() 两地的距离
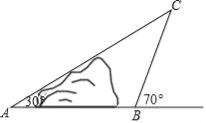
两地的距离![]() 长.(结果用含非特殊角的三角函数和根式表示即可)
长.(结果用含非特殊角的三角函数和根式表示即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:

(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件
商品以每件![]() 元出售,
元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 种商品数量的
种商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形中,是因式分解的是( )
A.x2﹣9+6x=(x+3)(x﹣3)+6x
B.6ab=2a3b
C.x2﹣8x+16=(x﹣4)2
D.(x+5)(x﹣2)=x2+3x﹣10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料 | 乙种原料 | |
维生素C含量(单位千克) | 600 | 100 |
原料价格(元千克) | 8 | 4 |
现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为x kg,则x应满足的不等式为( )
A.600x+100(10﹣x)≥4200
B.8x+4(100﹣x)≤4200
C.600x+100(10﹣x)≤4200
D.8x+4(100﹣x)≥4200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在小绿谷举办“民族团结一家亲”徒步活动,某人从起点出发,以4千米/小时的平均速度走了2小时到达终点,之后再沿原路返回,设此人离开起点的路程s(千米)与步行时间t(小时)之间的函数关系如图所示.根据图象提供信息,解答下列问题: 
(1)求图中的a值;
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C所用时间为1.75小时. ①求AB所在直线的函数解析式;
②求此人完成整个徒步过程所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市的出租车收费按里程计算,3km内(含3km)收费5元,超过3km,每增加1km加收1元,则路程x≥3时,车费y(元)与x(km)之间的关系式是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com