
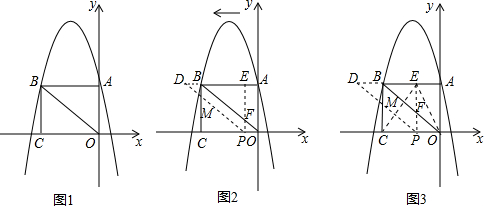
分析 (1)将点(0,3)和(-5,-2)代入即可求出b、c的值,进而得解,再由点A与点B对称可以求出点B的纵坐标为3,进而得解;
(2)根据平移的性质,以及垂直等条件,可以判断四边形EPCB是矩形,△BEF≌△PCM,进而可以用含有t的式子表示出四边形BFPM的面积,利用配方法可以得解;
(3)从OE=OC,EC=OC,OE=EC三个方面进行解答,即可得到本题的答案.
解答 解:(1)将点(0,3)和(5,-2)代入y=-x2+bx+c得:$\left\{\begin{array}{l}{c=3}\\{-25-5b+c=-2}\end{array}\right.$,
解得:b=-4,c=3,
∴y=-x2-4x+3,
(2)∵点B与点A关于对称轴对称,
∴B(-4,3);
由平移的性质可知,BO∥BD,OA∥PE,
∵OA⊥x轴,BC⊥x轴,
∴EP⊥x轴,
又AB∥OC,
∴∠EPC=∠BCP=∠BEP=∠EBC=90°,
∴四边形EPCB是矩形,
∴BE=PC,
∠ABO=∠BOC,∠BOC=∠MPC,
$\left\{\begin{array}{l}{BE=CP}\\{∠BEP=∠BCP}\\{∠ABO=∠MPC}\end{array}\right.$,
∴△BEF≌△PCM(ASA),
当△AOB向左平移运动的时间为t(s)时,
BE=4-t,EP=3,AE=t,
∴四边形EPCB的面积为:3(4-t),
设直线OB的解析式为y=kx,将点B(-4,3)代入得:
3=-4k,
解得:k=-$\frac{3}{4}$,
∴y=-$\frac{3}{4}$x,
∴F(t,-$\frac{3}{4}$t),
∴S△BEF=S△PCM=$\frac{1}{2}$(4-t)(3+$\frac{3}{4}$t),
四边形BFPM的面积为:
S=3(4-t)-(4-t)(3+$\frac{3}{4}$t)=-$\frac{3}{4}$(t-2)2+3,(0≤t≤4),
当t=2时,S有最大值,最大值是3;
(3)①当OE=EC时,AE=OP=$\frac{1}{2}$OC=2,此时E(-2,3).
②当OE=OC=4时,AE2+OA2=OE2=OC2,即:t2+9=16,
解得:t=$\sqrt{7}$或t=-$\sqrt{7}$(舍);此时E(-$\sqrt{7}$,3).
③当EC=OC=4时,
BE2+BC2=EC2,即:(4-t)2+9=16,
解得:t=4+$\sqrt{7}$(舍)或t=4-$\sqrt{7}$,此时E($\sqrt{7}$-4,3).
∴E的坐标为(-2,3)、(-$\sqrt{7}$,3)、($\sqrt{7}$-4,3).
点评 本题主要考查了用待定系数法求二次函数与一次函数的解析式,以及平移的性质,三角形全等、三角形面积的求法等知识点,是移动综合性很强的题目,有一定的难度,要注意认真总结.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
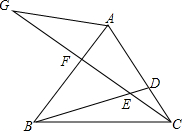 在等边△ABC中,D、F两点分别在边AC、AB上,AF=CD,连接BD、CF,并延长CF至点G,连接AG,且∠G=30°.若BE=10,CE=6,则CG=22.
在等边△ABC中,D、F两点分别在边AC、AB上,AF=CD,连接BD、CF,并延长CF至点G,连接AG,且∠G=30°.若BE=10,CE=6,则CG=22.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
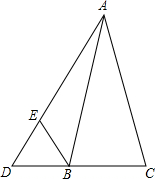 已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.
已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
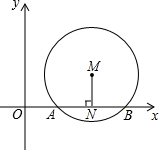 如图,在直角坐标系中,点M在第一象限内,MN⊥x轴于点N,MN=1,⊙M与x轴交于A(2,0)、B(6,0)两点.
如图,在直角坐标系中,点M在第一象限内,MN⊥x轴于点N,MN=1,⊙M与x轴交于A(2,0)、B(6,0)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com