
【题目】如图,在△ABC中,AM=CM,AD=CD,DM//BC,判断△CMB的形状,并说明理由.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】盐城市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利,小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图所示的统计图,请根据图中信息,解答下列问题:

(1)这次被调査的总人数是 ;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P与点Q都在y轴上,且关于x轴对称.
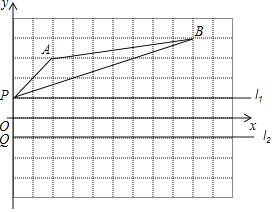
(1)请画出△ABP关于x轴的对称图形△A′B′Q(其中点A的对称点用A′表示,点B的对称点用B′表示);
(2)点P、Q同时都从y轴上的位置出发,分别沿l1、l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得AP+BQ=A′B成立?若存在,请你在图中画出此时PQ的位置(用线段P′Q′表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
查看答案和解析>>
科目:初中数学 来源: 题型:
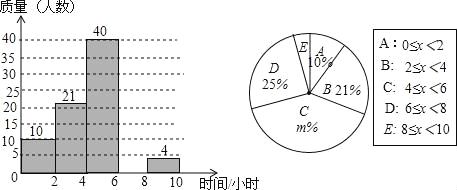
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
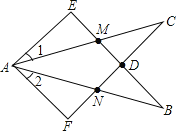
A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设美丽江城”的号召,我市某街道决定从备选的五种树中选购--种进行栽种。为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

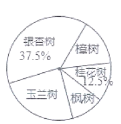
请根据所给信息解答以下问题:
(1)这次参与调查的居民总人数是多少人?
(2)此次调查的居民中最喜欢樟树的有多少人?请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:二元一次方程![]() 有无数组解,每组解记为
有无数组解,每组解记为![]() ,称
,称![]() 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
(1) 已知![]() ,则是隐线
,则是隐线![]() 的亮点的是 ;
的亮点的是 ;
(2) 设![]() 是隐线
是隐线![]() 的两个亮点,求方程
的两个亮点,求方程![]() 中
中![]() 的最小的正整数解;
的最小的正整数解;
(3)已知![]() 是实数, 且
是实数, 且![]() ,若
,若![]() 是隐线
是隐线![]() 的一个亮点,求隐线
的一个亮点,求隐线![]() 中的最大值和最小值的和.
中的最大值和最小值的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,AC交⊙O于点E,BC交⊙O于点D,F为CE的中点,连接DF.给出以下五个结论:①BD=DC;②AD=2DF;③ ![]() ;④DF是⊙O的切线.其中正确结论的个数是:( )
;④DF是⊙O的切线.其中正确结论的个数是:( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com