
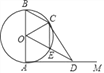
【题目】如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接OC、BC、CE.
(1)求证:CD是⊙O的切线;
(2)若圆O的直径等于2,填空:
①当AD= 时,四边形OADC是正方形;
②当AD= 时,四边形OECB是菱形.
【答案】(1)见解析;(2)①1;②![]() .
.
【解析】试题分析:(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;
(2)①依据正方形的四条边都相等可知AD=OA;
②依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.
试题解析:解:∵AM⊥AB,
∴∠OAD=90°.
∵OA=OC,OD=OD,AD=DC,
∴△OAD≌△OCD,
∴∠OCD=∠OAD=90°.
∴OC⊥CD,
∴CD是⊙O的切线.
(2)①∵当四边形OADC是正方形,
∴AO=AD=1.
故答案为:1.
②∵四边形OECB是菱形,
∴OE=CE.
又∵OC=OE,
∴OC=OE=CE.
∴∠CEO=60°.
∵CE∥AB,
∴∠AOD=60°.
在Rt△OAD中,∠AOD=60°,AO=1,
∴AD=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
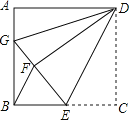
【题目】如图,正方形ABCD中,![]() ,点E在边BC上,
,点E在边BC上,![]() ,将
,将![]() 沿DE对折至
沿DE对折至![]() ,延长EF交边AB于点C,连接DG,BF,给出以下结论:
,延长EF交边AB于点C,连接DG,BF,给出以下结论:![]() ≌
≌![]() ;
;![]() ;
;![]() ;
;![]() ∽
∽![]() ,其中所有正确结论的个数是
,其中所有正确结论的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
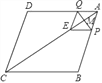
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“发展脐橙产业,加快脱贫的步伐”.某脐橙种植户新鮮采摘了20筐脐橙,以每筐25千克为标准重量,超过或不足干克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:干克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)与标准重量比较,20筐脐橙总计超过或不足多少千克?
(2)若脐橙毎干克售价6.5元,则出售这20筐脐橙可获得多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
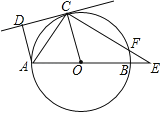
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上的一点,CE交⊙O于点F,连接OC,AC,若∠DAO=105°,∠E=30°.
(Ⅰ)求∠OCE的度数;
(Ⅱ)若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
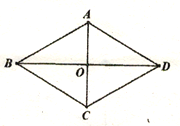
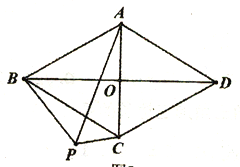
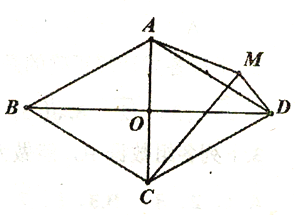
【题目】已知在菱形ABCD中,对角线AC、BD交于点O,AB=2AO;(1)如图1,求∠BAC的度数;(2)如图2,P为菱形ABCD外一点,连接AP、BP、CP,若∠CPB=120°,求证:CP+BP=AP;(3)如图3,M为菱形ABCD外一点,连接AM、CM、DM,若∠AMD=150°,
CM=2![]() ,DM=2,求四边形ACDM的面积。
,DM=2,求四边形ACDM的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程
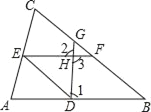
如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(________),
∴∠1+∠3=180°
∴______∥______(________)
∴∠B=______(________)
∵∠B=∠DEF(已知)
∴∠DEF=______(等量代换)
∴DE∥BC(________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①在数轴上表示![]() 的点一定在原点的左边;②有理数
的点一定在原点的左边;②有理数![]() 的倒数是
的倒数是![]() ;③一个数的相反数一定小于或等于这个数;④如果
;③一个数的相反数一定小于或等于这个数;④如果![]() ,那么
,那么![]() ;⑤
;⑤![]() 的次数是2;⑥有理数可以分为整数、正分数、负分数和0;⑦
的次数是2;⑥有理数可以分为整数、正分数、负分数和0;⑦![]() 与
与![]() 是同类项.其中正确的个数为( )
是同类项.其中正确的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com