
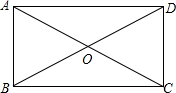
 如图,下列条件中,能使?ABCD成为矩形是( )
如图,下列条件中,能使?ABCD成为矩形是( )| A. | AB=AD | B. | ∠ABO=60° | C. | AO=BO | D. | AC⊥BD |
分析 由矩形的判定和菱形的判定方法即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
当AB=AD时,四边形ABCD是菱形,选项A错误;
∵四边形ABCD是平行四边形,
当∠ABO=60°时,四边形ABCD还是平行四边形,选项B错误;
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
当AO=BO时,AC=BD时,四边形ABCD是菱形,选项C正确;
∵四边形ABCD是平行四边形,
当AC⊥BD时,四边形ABCD是菱形,选项D错误;
故选:C.
点评 本题考查了对矩形的判定定理的应用,注意:矩形的判定定理有:①有一个角是直角的平行四边形是矩形,②有三个角是直角的四边形是矩形,③对角线相等的平行四边形是矩形.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x+3 | B. | y=-x+3 | C. | y=x+1 | D. | y=x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每周使用零花钱(单位:元) | 10 | 20 | 30 | 50 | 60 |
| 人 数 | 2 | 5 | 4 | 3 | 1 |
| A. | 5,4 | B. | 20,30 | C. | 5,5 | D. | 20,20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.5327×104 | B. | 1.5327×103 | C. | 1.5327×105 | D. | 1.5327×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com