
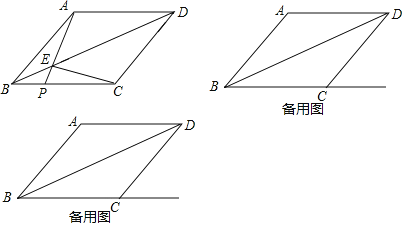
【题目】如图,菱形ABCD中,AB=20,连接BD,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
(1)求证:AE=CE;
(2)若sin∠ABD=![]() ,当点P在线段BC上时,若BP=8,求△PEC的面积;
,当点P在线段BC上时,若BP=8,求△PEC的面积;
(3)若∠ABC=45°,当点P在线段BC的延长线上时,请求出△PEC是等腰三角形时BP的长.
【答案】(1)见解析;(2)![]() ;(3)20
;(3)20![]() 或10
或10![]() +10
+10![]()
【解析】
(1)由SAS证得△ABE≌△CBE,即可得出结论;
(2)连接AC,交BD于O,求出OA=4![]() ,OB=8
,OB=8![]() ,则AC=8
,则AC=8![]() ,BD=16
,BD=16![]() ,S菱形ABCD=320,S△ABC=160,
,S菱形ABCD=320,S△ABC=160,![]() ,则S△ABP=
,则S△ABP=![]() S△ABC=64,易证∠ABE=∠PBE,得出
S△ABC=64,易证∠ABE=∠PBE,得出![]() ,则S△BPE=
,则S△BPE=![]() S△ABP=
S△ABP=![]() ,由
,由![]() ,得出S△PEC=
,得出S△PEC=![]() S△BPE即可得出结果;
S△BPE即可得出结果;
(3)①由(1)得△ABE≌△CBE,则∠BAE=∠BCE,当∠BAE=90°时,得△PEC是等腰直角三角形,过点E作∠FEC=45°交BC于F,则△FCE为等腰直角三角形,得出CE=CP=CF,EF=![]() CF,证明∠BEF=∠EBC,得出EF=BF,则
CF,证明∠BEF=∠EBC,得出EF=BF,则![]() CF+CF=BC=20,求出CF=20(
CF+CF=BC=20,求出CF=20(![]() ﹣1),即可得出结果;
﹣1),即可得出结果;
②由(1)得△ABE≌△CBE,则∠AEB=∠CEB,当∠BAE=105°时,∠AEB=52.5°,得出∠AEC=105°,∠CEP=75°,证明∠ECP=∠CEP,得出△PEC是等腰三角形,过点A作AN⊥BP于N,则△ABN是等腰直角三角形,得出AN=BN=![]() AB=10
AB=10![]() ,由tan30°=
,由tan30°=![]() ,求出PN=10
,求出PN=10![]() ,即可得出结果.
,即可得出结果.
(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=BC,
在△ABE和△CBE中,
 ,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:连接AC,交BD于O,如图1所示:
∵四边形ABCD是菱形,
∴∠AOB=90°,OB=OD,OA=OC,AB=BC=20,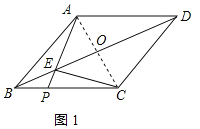
∵sin∠ABD=![]() ,
,
∴OA=4![]() ,
,
∴AC=2OA=2×4![]() =8
=8![]() ,
,
BD=2OB=2×8![]() =16
=16![]() ,
,
∴S菱形ABCD=![]() ACBD=
ACBD=![]() ×8
×8![]() ×16
×16![]() =320,
=320,
∴S△ABC=![]() S菱形ABCD=
S菱形ABCD=![]() ×320=160,
×320=160,
∵BP=8,
∴CP=BC-BP=20-8=12,
∵![]() ,
,
∴S△ABP=![]() S△ABC=
S△ABC=![]() ×160=64,
×160=64,
∵四边形ABCD是菱形,
∴∠ABE=∠PBE,
∴点E到边AB、BP的距离相等,
∴![]() ,
,
∴S△BPE=![]() S△ABP=
S△ABP=![]() ×64=
×64=![]() ,
,
∵![]() ,
,
∴S△PEC=![]() S△BPE=
S△BPE=![]() ×
×![]() =
=![]() ;
;
(3)解:①由(1)得:△ABE≌△CBE,
∴∠BAE=∠BCE,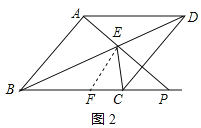
当∠BAE=90°时,则∠BCE=90°,
∴∠ECP=90°,
∵∠ABC=45°,
∴∠EBC=22.5°,∠CPE=45°,
∴△PEC是等腰直角三角形,
∴CE=CP,∠BEC=90°-22.5°=67.5°,
过点E作∠FEC=45°交BC于F,如图2所示:
则△FCE为等腰直角三角形,
∴CE=CP=CF,EF=![]() CF,∠BEF=∠BEC-∠FEC=67.5°-45°=22.5°,
CF,∠BEF=∠BEC-∠FEC=67.5°-45°=22.5°,
∴∠BEF=∠EBC,
∴EF=BF,
∴![]() CF+CF=BC=20,
CF+CF=BC=20,
∴CF=![]() =20(
=20(![]() -1),
-1),
∴BP=BC+CP=BC+CF=20+20(![]() -1)=20
-1)=20![]() ;
;
②由(1)得:△ABE≌△CBE,
∴∠AEB=∠CEB,
当∠BAE=105°时,∠AEB=180°-105°-22.5°=52.5°,
∴∠AEC=2∠AEB=105°,
∴∠CEP=180°-105°=75°,
∵∠APB=180°-105°-45°=30°,
∴∠ECP=180°-75°-30°=75°,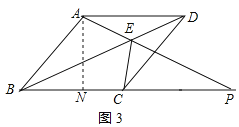
∴∠ECP=∠CEP,
∴△PEC是等腰三角形,
过点A作AN⊥BP于N,如图3所示:
则△ABN是等腰直角三角形,
∴AN=BN=![]() AB=10
AB=10![]() ,
,
∵∠APB=30°,
∴tan30°=![]() ,即
,即![]() ,
,
∴PN=10![]() ,
,
∴BP=BN+PN=10![]() +10
+10![]() ;
;
综上所述,△PEC是等腰三角形时BP的长为20![]() 或10
或10![]() +10
+10![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了缓解市区日益拥堵的交通状况,长沙市地铁建设工程指挥部对长沙地铁4号线茶子山站工程进行招标,接到了甲、乙两个工程队的指标书,从指标书中得知:甲工程队单独完成这项工程所需的时间是乙队单独完成这项工程所需的时间的3倍,若由甲队先做2个月,剩下的工程由甲、乙两队合作4个月可以完成.
(1)求甲、乙两队单独完成这项工程各需几个月?
(2)已知甲队每月的施工费用是76万元,乙队每月的施工费用是164万元,工程预算的施工费用为1000万元,为缩短工期以减少队交通的影响,拟安排甲、乙两队合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出拟的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
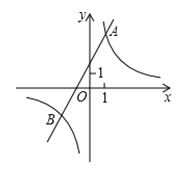
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
(1)求这两个函数的关系式;
(2)观察图象,直接写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0),(3,0)两点,则下列判断中,错误的是( )

A.图象的对称轴是直线x=1
B.当﹣1<x<3时,y<0
C.当x>1时,y随x的增大而减小
D.一元二次方程中ax2+bx+c=0的两个根是﹣1和3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=![]() ,AB=10,求AE的长;
,AB=10,求AE的长;
(3)若△CDE的面积是△OBF面积的![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.∠ABC的平分线交AC于点O,以点O为圆心,OC为半径.在△ABC同侧作半圆O.
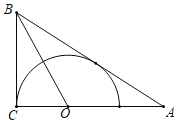
(1)求证:AB与⊙O相切;
(2)若AB=5,AC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售每台进价分别为400元、340元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 3600元 |
第二周 | 4台 | 10台 | 6200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若该商场准备用不多于1.14万元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
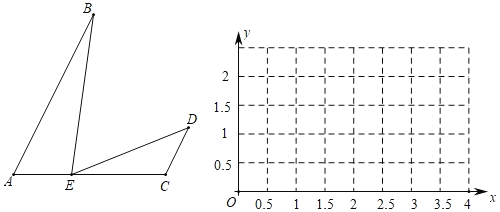
【题目】如图,AB∥CD,AB=5cm,AC=4cm,线段AC上有一动点E,连接BE,ED,∠BED=∠A=60°,设A,E两点间的距离为xcm,C,D两点间的距离为ycm.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.3 | 2.5 |
y/cm | 0 | 0.39 | 0.75 | 1.07 | 1.33 | 1.45 |
|
x/cm | 2.8 | 3.2 | 3.5 | 3.6 | 3.8 | 3.9 | |
y/cm | 1.53 | 1.42 | 1.17 | 1.03 | 0.63 | 0.35 |
请你补全表格;
(2)描点、连线:在平面直角坐标系xOy中,描出表中各组数值所对应的点(x,y),并画出函数y关于x的图象;
(3)探究性质:随着自变量x的不断增大,函数y的变化趋势: ;
(4)解决问题:当AE=2CD时,CD的长度大约是 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com