练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，个边长为的相邻正方形的一边均在同一直线上，点，，，…分别为边，，，…，的中点，的面积为，的面积为，…的面积为，则________．（用含的式子表示）

    【答案】

    【解析】

    由n个边长为1的相邻正方形的一边均在同一直线上，点M1，M2，M3，…Mn分别为边B1B2，B2B3，B3B4，…，BnBn+1的中点，即可求得△B1C1Mn的面积，又由BnCn∥B1C1，即可得△BnCnMn∽△B1C1Mn，然后利用相似三角形的面积比等于相似比的平方，求得答案．

    ∵n个边长为1的相邻正方形的一边均在同一直线上,点M1，M2，M3，…Mn分别为边B1B2，B2B3，B3B4，…，BnBn+1的中点，

    ∴

    ∵BnCn∥B1C1，

    ∴△BnCnMn∽△B1C1Mn，

    ∴

    即

    ∴

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在RtABC 中，ACB 90 ， AC 3 ，BC 4 ，点 D在 AB上， AD AC ， AF CD 交CD 于点 E ，交CB 于点 F ，则CF 的长是( )

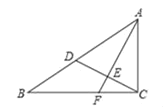
    A. 2.5B. 2C. 1.8D. 1.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】几何模型：

    条件：如图1，A、B是直线同旁的两个定点．

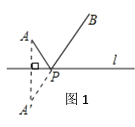
    问题：在直线上确定一点P，使PA+PB的值最小．

    方法：作点A关于直线的对称点A′，连接A′B交于点P，则PA+PB=A′B的值最小（不必证明）．

    模型应用：

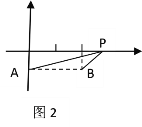
    （1）如图2,已知平面直角坐标系中两定点A（0，-1），B（2，-1）,P为x轴上一动点, 则当PA+PB的值最小时，点P的横坐标是______，此时PA+PB的最小值是______；

    （2）如图3，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点.由正方形对称性可知，B与D关于直线AC对称，连接BD，则PB+PE的最小值是______；

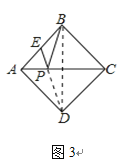
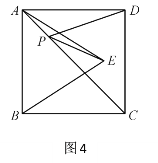
    （3）如图4,正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD＋PE的最小值为 ；

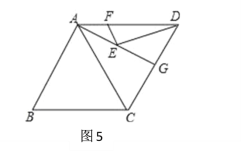
    （4）如图5,在菱形ABCD中，AB=8，∠B=60°，点G是边CD边的中点，点E、F分别是AG、AD上的两个动点，则EF+ED的最小值是_______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与直线交于点．

    （1）求m的值；

    （2）方程组的解是________；

    （3）直线是否也经过点P？请判断并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

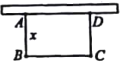
    【题目】如图，有长为24m的篱笆，围成长方形的花圃，且花圃的一边为墙体（墙体的最大可用长度为20m）。

    设花圃的面积为AB的长为xm.

    （1）求y与x函数关系式，并写出x的取值范围；

    （2）x为何值时，y取得最大值？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某市近郊有一块长为60米，宽为50米的矩形荒地，地方政府准备在此建一个综合性休闲广场，其中阴影部分为通道，通道的宽度均相等，中间的三个矩形（其中三个矩形的一边长均为a米）区域将铺设塑胶地面作为运动场地．设通道的宽度为x米．

    （1）a＝ （用含x的代数式表示）；

    （2）若塑胶运动场地总占地面积为 2430平方米，则通道的宽度为多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据农业农村部消息，国内受猪瘟与猪周期叠加影响，生猪供应量大幅减少，从今年6月起猪肉价格连续上涨一品生鲜超市在6月1日若售出五花肉和排骨，销售额为366元；若售出五花肉和排骨，销售额为186元.

    （1）6月1日每千克五花肉和排骨的价格各是多少元？

    （2）6月1日五花肉和排骨的销售量分别为、由于猪肉价格持续上涨，11月1日五花肉的销售价格在6月1日的基础上增长了，销售量减少了；排骨的销售价格在6月1日的基础上增加了元，销售量下降了.结果1l月1日的销售额比6月1日的销售额多5100元，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

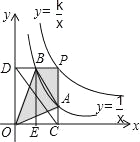
    【题目】两个反比例函数y=（k＞1）和y=在第一象限内的图象如图所示，点P在y=的图象上，PC⊥x轴于点C，交y=的图象于点A，PD⊥y轴于点D，交y=的图象于点B，BE⊥x轴于点E，当点P在y=图象上运动时，以下结论：①BA与DC始终平行；②PA与PB始终相等；③四边形PAOB的面积不会发生变化：④△OBA的面积等于四边形ACEB的面积．其中一定正确的是_____．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在△ABC中, AD是∠BAC的平分线，DF⊥AB，DM⊥AC，垂足分别为F、M，AF=10cm ，BF=6cm ，AC=14cm.动点E以3cm/s的速度从A点向B点运动，动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t s.当t=__________s时, △DFE与△DMG全等.(写出符合题意的t的所有取值)

    查看答案和解析>>

    同步练习册答案