
��ͼ�����������в����ж���ACD�ס�ABC���ǣ� ��

A.  B. ��ADC����ACB
B. ��ADC����ACB
C. ��ACD����B D. AC2=AD��AB
A ���������������߶�Ӧ�ɱ����Ҽн���ȣ����ɣ���B=��B���ɵá�ACD�ס�ABC����A�����ж������������ƣ� �������Ƕ�Ӧ��ȵ������������ƣ���֪B��C�������ж������������ƣ��������߶�Ӧ�ɱ����Ҽн���ȣ�����AC2=AD��AB����AΪ�����ǣ����ж�������������. ��ѡ��A. ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ� ȫ���ۺϲ��Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���C��40�㣬����ABC����ֱ��l�۵�����C���ڵ�D��λ�ã����1����2�Ķ����ǣ� ��

A. 40�� B. 80�� C. 90�� D. 140��
B �������� ������ã���C=��D�� �ߡ�1=��C+��3����3=��2+��D�� ���1=��2+��C+��D=��2+2��C�� ���1����2=2��C=80��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ���ѡ��
��ͼ����������ֽƬABCD�۵���ʹ��DC���ڶԽ���AC�ϣ��ۺ�ΪCE����D�����ڶԽ�����D'��.��AB=3��AD=4����ED�ij�Ϊ(����)

A.  B. 3 C. 1 D.
B. 3 C. 1 D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����Ϻӿ���2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�������EDCF����������E��D��F���������εı��ϣ���һ������C�������εĶ����غϣ���AC=4��BC=6����ED�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����Ϻӿ���2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��֪tanA= �������A�Ķ�����__________��
�������A�Ķ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����Ϻӿ���2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
һԪ���η���x2��6x��5=0�䷽�ɱ���Ϊ��������
A. ��x��3��2=14 B. ��x��3��2=4 C. ��x+3��2=14 D. ��x+3��2=4
A �����������������x2��6x��5=0���ѷ��̵ij������Ƶ��ұߵã�x2��6x=5���������߶�����32�ã�x2��6x+9=5+9�����ԣ�x��3��2=14���ʴ�ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ������
(8��)�ⷽ�̣�
(1)2(x��3)����3(x��1)��2; (2) 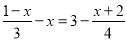 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ������
�ۺ���̽��
��ͼ����ƽ��ֱ������ϵxOy�У�������W�ĺ�������ʽΪy=��x2+2x+3��������W��x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C�����Ķ���ΪD��ֱ��l����A��C���㣮
��1�����A��B��C��D�����꣮
��2����ֱ��l����ƽ��m����λ����Ӧ��ֱ��Ϊl�䣮
����ֱ��l����x��������ύ�ڵ�E����y��������ύ�ڵ�F����AEF�����ΪS����S����m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
����m��ֵΪ����ʱ��S��ֵ������ֵΪ���٣�
��3������������WҲ����ƽ��m��λ��������ƽ��1����λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ���P���ڡ�AOC���ڲ�����������AOC�ı߽磩����ֱ��д��m��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ���ѡ��
һ�˳�ѩ�����±�1��  ��б�±�ֱ���£����µľ���s��m����ʱ��t��s����Ĺ�ϵΪs=10t+2t2���������µ�ʱ��Ϊ4s��������½��ĸ߶�Ϊ��������
��б�±�ֱ���£����µľ���s��m����ʱ��t��s����Ĺ�ϵΪs=10t+2t2���������µ�ʱ��Ϊ4s��������½��ĸ߶�Ϊ��������

A. 72m B. 36 m C. 36m D. 18
m C. 36m D. 18 m
m
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com