

 摄制组在拍摄中心C出发,乘船到达码头B后,立即返回.求船只往返B、C两处所用的时间.
摄制组在拍摄中心C出发,乘船到达码头B后,立即返回.求船只往返B、C两处所用的时间.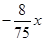 (3)
(3)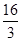
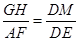 ,即
,即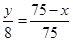 ,
,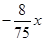 . …………………………………………………7分
. …………………………………………………7分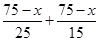 ,即y=8
,即y=8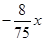 .(此解法也相应给3分)
.(此解法也相应给3分)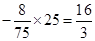 (小时).……………………10分
(小时).……………………10分

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源:不详 题型:解答题
 的取值范围;
的取值范围;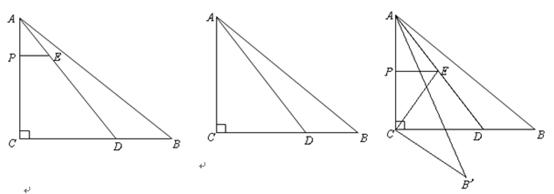
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
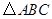 的位似图形
的位似图形 ,使
,使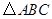 与
与 的位似比等于
的位似比等于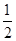 ,则点
,则点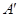 的坐标为 .
的坐标为 .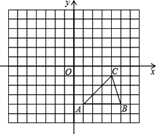
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
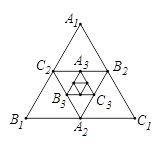
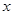 秒。
秒。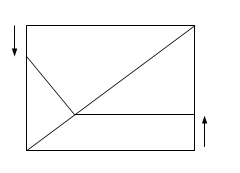
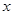 的代数式表示)
的代数式表示)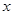 ≤3秒,试求△MPA的面积S与时间
≤3秒,试求△MPA的面积S与时间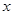 秒的函数关系式,并求S的最大值。
秒的函数关系式,并求S的最大值。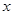 ≤3秒,△MPA能否与△PCN相似?若能,试求出相似时
≤3秒,△MPA能否与△PCN相似?若能,试求出相似时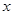 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com