
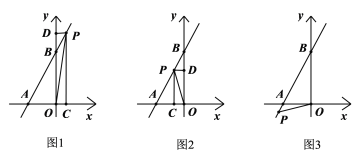
【题目】如图,已知直线l:y=2x+4交x轴于A,交y轴于B.

(1) 直接写出直线l向右平移2个单位得到的直线l1的解析式_______;
(2) 直接写出直线l关于y=-x对称的直线l2的解析式_______;
(3) 点P在直线l上,若S△OAP=2S△OBP,求P点坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点P的坐标为
;(3)点P的坐标为![]() 或
或![]() .
.
【解析】
(1)根据一次函数的图象平移规律即可得;
(2)先求出点A、B的坐标,再求出点A、B关于![]() 对称点的坐标,然后利用待定系数法求解即可得;
对称点的坐标,然后利用待定系数法求解即可得;
(3)设点P的坐标为![]() ,分点P在直线
,分点P在直线![]() 第一象限的图象上、点P在直线
第一象限的图象上、点P在直线![]() 第二象限的图象上、点P在直线
第二象限的图象上、点P在直线![]() 第三象限的图象上,再根据
第三象限的图象上,再根据![]() ,利用三角形的面积公式列出等式求解即可得.
,利用三角形的面积公式列出等式求解即可得.
(1)一次函数![]() 的图象平移规律:向左(或向右)平移a个单位长度得到的函数解析式为
的图象平移规律:向左(或向右)平移a个单位长度得到的函数解析式为![]() (或
(或![]() );向上(或向下)平移a个单位长度得到的函数解析式为
);向上(或向下)平移a个单位长度得到的函数解析式为![]() (或
(或![]() )
)
则直线![]() 向右平移2个单位得到的直线
向右平移2个单位得到的直线![]() 的解析式为
的解析式为![]() ,即
,即![]()
故答案为:![]() ;
;
(2)对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,则
,则![]()
当![]() 时,
时,![]() ,则
,则![]()
由对称性可知,点![]() 关于直线
关于直线![]() 对称点坐标为
对称点坐标为![]() ;点
;点![]() 关于直线
关于直线![]() 对称点坐标为
对称点坐标为![]()
设直线![]() 的解析式为
的解析式为![]()
将点![]() ,
,![]() 代入得:
代入得: ,解得
,解得
则直线![]() 的解析式为
的解析式为![]()
故答案为:![]() ;
;
(3)设点P的坐标为![]()
![]()
![]()
因为点P在直线![]() 上,则分以下三种情况:
上,则分以下三种情况:
①如图1,点P位于直线![]() 第一象限的图象上
第一象限的图象上
则有![]() ,解得
,解得![]()
过点P作![]() 轴于点C,作
轴于点C,作![]() 轴于点D
轴于点D
则![]()
![]()
![]()
由![]() 得:
得:![]() ,解得
,解得![]() (符合题设)
(符合题设)
![]()
此时,点P的坐标为![]()
②如图2,点P位于直线![]() 第二象限的图象上
第二象限的图象上
则有![]() ,解得
,解得![]()
过点P作![]() 轴于点C,作
轴于点C,作![]() 轴于点D
轴于点D
则![]()
![]()
![]()
由![]() 得:
得:![]() ,解得
,解得![]() (符合题设)
(符合题设)
![]()
此时,点P的坐标为![]()
③如图3,点P位于直线![]() 第三象限的图象上
第三象限的图象上
![]()
此时,不可能存在点P,使得![]()
综上,点P的坐标为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在我市“青山绿水”行动中,某社区计划对面积为![]() 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为
的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
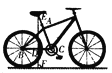
【题目】如图所示的是一辆自行车的侧面示意图.已知车轮直径为65 cm,车架中AC的长为42 cm,座杆AE的长为18 cm,点E,A,C在同一条直线上,后轴轴心B与中轴轴心C所在直线BC与地面平行,∠C=73°,求车座E到地面的距离EF.(结果精确到l cm,参考数据:sin 73°≈0.96,cos 73°≈0.29,tan 73°≈3.27)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:据说,我国著名数学家华罗庚在出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39,邻座的乘客十分惊奇,忙问计算的奥妙.
你知道华罗庚是怎样迅速准确地计算出来的吗?他是按照下面的方法确定的:
由![]() ,
,![]() ,就能确定
,就能确定![]() 是2位数.由59319的个位上的数是9,就能确定
是2位数.由59319的个位上的数是9,就能确定![]() 的个位上的数是9,如果划去59319后面的三位319得到数59,而
的个位上的数是9,如果划去59319后面的三位319得到数59,而![]() ,
,![]() ,由此可确定
,由此可确定![]() 的十位上的数是3,所以,
的十位上的数是3,所以,![]() .
.
(1)已知19683,110592都是整数的立方,按照上述方法,请直接写出它们的立方根;
(2)![]() 是我们没有学习过的四次方根,且它的结果也是一个整数,请你根据材料的方法求出结果,并说明理由.
是我们没有学习过的四次方根,且它的结果也是一个整数,请你根据材料的方法求出结果,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一根绳子平放在桌上,用剪刀任意剪n刀(如图①),绳子变成n+1段;若将绳子对折1次后从中间剪一刀(如图②),绳子的刀口 个,绳子变成 段;若将绳子对折2次后从中间剪一刀,绳子的刀口有 个,绳子变成 段;若将绳子对折n次后从中间剪一刀,绳子的刀口 个,绳子变成 段.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=1,E是BC上一点,将△DCE沿DE翻折得到△DC′E.

(1) 如图1,若点B恰好在DC′的延长线上,且C′B=C′D,求CE的长;
(2) 如图2,若点A恰好在EC′的延长线上,且C′A=2C′E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )


A. A B. B C. C D. D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com