
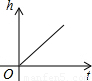
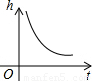
 gt2,(g为正常数,t为时间),则函数图象为( )
gt2,(g为正常数,t为时间),则函数图象为( )

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:中华题王 数学 九年级上 (北师大版) 北师大版 题型:044
为了预防“非典”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图所示).现测得药物8 min燃毕,此时室内空气中每立方米的含药量为6 mg请根据题中所提供的信息,解答下列问题.
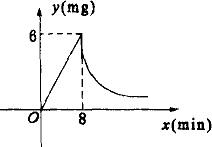
(1)药物燃烧时,y关予x的函数关系式为________,自变量x的取值范围是:________;药物燃烧后,y关于x的函数关系式为:________;
(2)研究表明,当空气中每立方米的含药量低于1.6 mg时学生方可进教室,那么从消毒开始,至少需要经过________min后,学生才能回到教室;
(3)研究表明,当空气每立方米的含药量低于3 mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川乐山卷)数学 题型:解答题
如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点
P与点C不重合),连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得
到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.
(1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 ▲ 关
系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△
AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面积为
S,求S关于x的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:1997年江苏省南京市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com