Question

15．正方形ABDE中，AB=2，以AB为边作等边△ACB，BF⊥AC于F，直线DC交直线BF于M，则CD=$\sqrt{6}±\sqrt{2}$．

Answer 1

分析 根据题意画出图形，分△ACB在正方形的内部和外部两种情况考虑，再根据勾股定理解答即可．

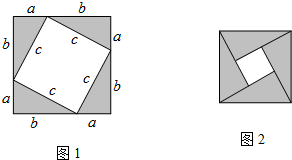
解答 解：当△ACB在正方形ABDE内部时，如图1：

过点C作CG⊥BD，
∵等边△ACB，BF⊥AC于F，
∴∠FBC=30°，∠BFC=90°，∠ABC=60°，
∵正方形ABDE中，AB=2，
∴∠CBG=90°-60°=30°，
在△BFC和△BGC中，
$\left\{\begin{array}{l}{∠BFC=∠BGC}\\{∠FBC=∠GBC}\\{BC=BC}\end{array}\right.$，
∴△BFC≌△BGC（AAS），
∴CG=CF，BF=BG，
∵正方形ABDE中，AB=2，以AB为边作等边△ACB，BF⊥AC于F，
∴BG=$\sqrt{3}$，CG=1，
∴GD=2-$\sqrt{3}$，CG=1，
∴CD=$\sqrt{（2-\sqrt{3}）^{2}+1}=\sqrt{8-4\sqrt{3}}=\sqrt{6}-\sqrt{2}$，
当△ACB在正方形ABDE外部时，如图2：

过点C作CH⊥BD，
∵等边△ACB，BF⊥AC于F，
∴∠FBC=30°，∠BFC=90°，∠ABC=60°，
∵正方形ABDE中，AB=2，
∴∠CBH=90°-60°=30°，
在△BFC和△BHC中，
$\left\{\begin{array}{l}{∠BFC=∠BHC}\\{∠FBC=∠HBC}\\{BC=BC}\end{array}\right.$，
∴△BFC≌△BHC（AAS），
∴CH=CF，BF=BH，
∵正方形ABDE中，AB=2，以AB为边作等边△ACB，BF⊥AC于F，
∴BH=$\sqrt{3}$，CH=1，
∴HD=2+$\sqrt{3}$，CH=1，
∴CD=$\sqrt{（2+\sqrt{3}）^{2}+1}=\sqrt{8+4\sqrt{3}}=\sqrt{6}+\sqrt{2}$，
综上所述，CD=$\sqrt{6}±\sqrt{2}$，
故答案为：$\sqrt{6}±\sqrt{2}$．

点评 此题考查正方形的问题，关键是利用正方形的性质和等边三角形的性质分析，同时作出正确图形分情况解题是难点．